��Ŀ����
����Ŀ����ͼ��ʾ��һ��Һ������Զ������ʾ��ͼ���������ĵײ�ˮƽ����һƽ�澵����ƽ�澵�Ϸ���һ������ƽ�澵ƽ�У�������������һ��������60�������ǵ�Һƽ���ϣ�����Һ���еĹ��߾�ƽ�澵������ٴ�Һ����ϱ�����������������γ�һ���㣬Һ�����ȱ仯����������������ƶ���2 ![]() dm����֪��Һ���������n=
dm����֪��Һ���������n= ![]() ������й���c=3.0��108m/s�������Ǿ�Һ�淴��Ĺ��ߣ���
������й���c=3.0��108m/s�������Ǿ�Һ�淴��Ĺ��ߣ���
��Һ��߶ȵı仯����
��Һ�����ȱ仯ǰ��ӷ����������ϵ�ʱ��仯�˶��٣�
���𰸡��⣺�ٹ�·ͼ��ʾ��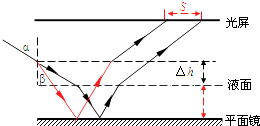
�������Ϊ���������Ϊ�£�ԭ��Һ�����Ϊh��Һ��������ӡ�h�����Ϲ���ƶ��ľ���
s=2 ![]() dm
dm
�������䶨�� n= ![]() �� ��=30��
�� ��=30��
�ɼ��ι�ϵ��
2htan��+2��htan��=2����h+h��tan��+s
�á�h= ![]()
�����á�h=1.5dm
�ڹ��ڸ�Һ���еĴ����ٶ�Ϊ v= ![]() =
= ![]() m/s
m/s
Һ�����ȱ仯ǰ��ӷ����������ϵ�ʱ��仯Ϊ��t= ![]() ��
�� ![]() =0
=0
�𣺢�Һ��߶ȵı仯��Ϊ1.5dm��
��Һ�����ȱ仯ǰ��ӷ����������ϵ�ʱ��仯��0��
���������ٻ�����·ͼ��ͨ����ѧ���ι�ϵ������䶨�����Һ��߶ȵı仯�����ڸ���v= ![]() �������Һ���д������ٶȴ�С���ֱ��������Һ����ȱ仯ǰ���������߶���ι��������е�ʱ�䣬�Ӷ����ʱ��ı仯����
�������Һ���д������ٶȴ�С���ֱ��������Һ����ȱ仯ǰ���������߶���ι��������е�ʱ�䣬�Ӷ����ʱ��ı仯����
�����㾫����������Ҫ�����˹����������֪ʶ�㣬��Ҫ���չ���һ�ֽ���������һ�ֽ���ʱ�������ֽ��ʵĽ����Ͻ�������Ĵ�������ı������й�����������ȷ�����⣮

 100�ִ�����ĩ���ϵ�д�
100�ִ�����ĩ���ϵ�д�