题目内容
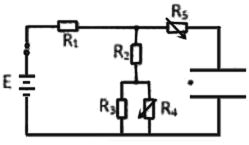
【题目】如图所示,电源电动势E=3V,内阻不计,R1、R2、R3为定值电阻,阻值分别为1Ω、0.5Ω、9Ω、R4、R5为电阻箱,最大阻值均为99.9Ω,右侧竖直放置一个电容为1.5×10﹣3μF的理想平行板电容器,电容器板长0.2m,板间距为0.125m。一带负电粒子以0.8m/s的速度沿平行板中线进入,恰好匀速通过,不计空气阻力,此时R4、R5阻值分别为1.8Ω、1Ω.试求:
(1)带电粒子匀速穿过电容器时,求电容器的电荷量为多少?
(2)欲使粒子向上偏转但又不打到电容器的上板,R4阻值不得超过多少Ω?
(3)欲使粒子向下偏转但又不打到电容器的下板,R4阻值不得低于多少Ω?
【答案】(1)3×10﹣9C(2)5.7Ω(3)0.69Ω
【解析】
(1)电容器与R2、R3、R4这部分电路并联,当粒子匀速穿过电容器时,R2、R3、R4这部分电路的总电阻为:
![]() ,
,
根据串联电路分压特点可得这部分的电压
![]() ,
,
电容器的电荷量为
![]() 。
。
(2)当粒子匀速穿过电容器时,有
![]() ,
,
粒子在电容器中的运动时间
![]() ;
;
当粒子向上偏转且刚好经过上极板最右端时,
在竖直方向上,有
![]() ,
,
解得:
a=2m/s2.
由牛顿第二定律得
![]() ,
,
可得
![]() ,
,
并可得
![]() ,
,
由此得R2、R3、R4这部分电路总电压
U1=2.4V,
R1的电压
![]() ,
,
电流
![]() ,
,
可得R2、R3、R4这部分电路总电阻
![]() ,
,
由
![]() ,
,
由此算出
R4≈5.7Ω,
所以欲使粒子向上偏转但又不打到电容器的上板,R4阻值不得超过5.7Ω
(3)当粒子向下偏转且刚好经过下极板最右端时,
在竖直方向上,有
![]() ,
,
解得:
a=2m/s2.
由牛顿第二定律得
![]() ,
,
可得
![]() ,
,
并可得
![]() ,
,
由此得R2、R3、R4这部分电路总电压
U2=1.6V,
R1的电压
![]() ,
,
电流
![]() ,
,
可得R2、R3、R4这部分电路总电阻
![]() ,
,
由
![]() ,
,
由此算出
R4≈0.69Ω,
所以欲使粒子向上偏转但又不打到电容器的上板,R4阻值不得超过0.69Ω