题目内容
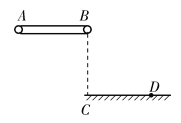
【题目】有一水平传送带AB长L=8 m,距离水平地面h=![]() m,地面上C点在传送带右端点B的正下方.一小物块以水平初速度
m,地面上C点在传送带右端点B的正下方.一小物块以水平初速度![]() =2 m/s自A点滑上传送带,它与传送带间的动摩擦因数μ=0.2,传送带以恒定速率
=2 m/s自A点滑上传送带,它与传送带间的动摩擦因数μ=0.2,传送带以恒定速率![]() 顺时针运行 .(g取10 m/s2)
顺时针运行 .(g取10 m/s2)
(1)若传送带运行速率![]() =3m/s, 求小物块落地时速度大小和方向;
=3m/s, 求小物块落地时速度大小和方向;
(2)若传送带运行速率![]() =1m/s, 求小物块从滑上传送带到落地所用时间;
=1m/s, 求小物块从滑上传送带到落地所用时间;
(3)当传送带运行速率![]() 满足什么要求时,小物块落地点D到C的距离最远?并求出这个最远距离。
满足什么要求时,小物块落地点D到C的距离最远?并求出这个最远距离。
【答案】(1) ![]() 与水平方向的夹角为
与水平方向的夹角为![]()
(2)![]()
(3)![]() 最远距离为
最远距离为![]()
【解析】(1)小物块的初速度小于3m/s,所以刚放上时做匀加速直线运动,加速度![]()
小物块加速到和传送带速度相同时和传送带发生的相对位移为![]()
故小物块加速到3m/s时和传送带一块做匀速直线运动,故从B点抛出的初速度为3m/s
小物块从B点做平抛运动,故落地的速度为![]() ,与水平方向的夹角为
,与水平方向的夹角为![]() ,
, ![]() ,即与水平方向夹角为45°
,即与水平方向夹角为45°
(2)若传送带运行速率为![]() ,则小物块的速度大于传送带的速度,所以刚放上时做匀减速直线运动,加速度
,则小物块的速度大于传送带的速度,所以刚放上时做匀减速直线运动,加速度![]() ,
,
小物块减速到和传送带速度相同时和传送带发生的相对位移为![]() ,即小物块在传送带上先减速后匀速运动,然后做平抛运动,经历的时间为
,即小物块在传送带上先减速后匀速运动,然后做平抛运动,经历的时间为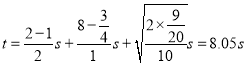
(3)要使小物块落地点D到C的距离最远,则要求小物块从B点抛出的速度最大,故当小物块一直在传送带上加速运动时,到达B点的速度最大,所以有![]() ,解得
,解得![]() ,即要求传送带的速度
,即要求传送带的速度![]()
最远距离为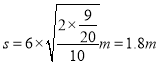

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目