题目内容
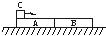
如图,质量为0.5kg、长1.2m的金属盒AB,放在水平桌面上,它与桌面间动摩擦因数μ=0.125。在盒内右端B处放着质量也为0.5kg、半径为0.1m的小球,球与盒间无摩擦。若在A端给盒以水平向右的冲量1.5N·s,设盒在运动中与球碰撞时间极短,且无能量损失,求:
(1)盒从开始运动到完全停止所通过的路程是多少?
(2)盒从开始运动到完全停止所经过的时间是多少?

(1)盒从开始运动到完全停止所通过的路程是多少?
(2)盒从开始运动到完全停止所经过的时间是多少?

(1)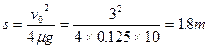
(2)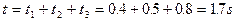
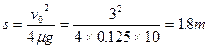
(2)
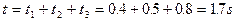
(1)盒的初速度:
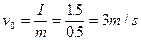
盒从开始运动到完全停止的过程中,盒的初动能全部转化为因摩擦所产生的内能,所以:
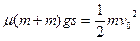
所以盒通过路程为:
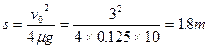
(2)从盒开始运动到第一次碰撞的t1时间内,球静止,盒减速运动,对盒有:
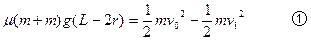

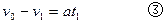
由①②③得:t1=0.4s,v1=2m/s
球与盒碰撞后二者交换速度,球再经时间t2与盒第二次碰撞。所以:
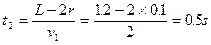
二者碰后再次交换速度,盒再运动时间t3停下,所以:at3=v1
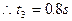
t3时间内盒子位移:

所以盒子至停止运动不再和球发生碰撞,因此盒从开始运动到停下所用总时间:
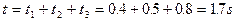
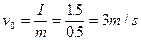
盒从开始运动到完全停止的过程中,盒的初动能全部转化为因摩擦所产生的内能,所以:
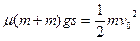
所以盒通过路程为:
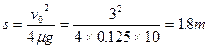
(2)从盒开始运动到第一次碰撞的t1时间内,球静止,盒减速运动,对盒有:
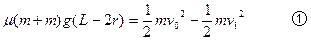

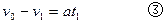
由①②③得:t1=0.4s,v1=2m/s
球与盒碰撞后二者交换速度,球再经时间t2与盒第二次碰撞。所以:
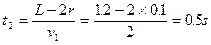
二者碰后再次交换速度,盒再运动时间t3停下,所以:at3=v1
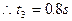
t3时间内盒子位移:

所以盒子至停止运动不再和球发生碰撞,因此盒从开始运动到停下所用总时间:
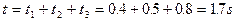

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目