题目内容
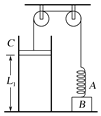
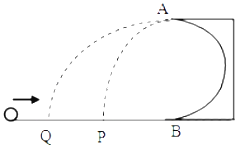
【题目】如图所示,有一质量为M=2. 0kg、内表面光滑的水平金属盒,其长度L=1.4m,静止放置在粗糙且较大的水平桌面上,在水平金属盒的左、右两端各有一个挡板,金属盒与水平桌面间的动摩擦因数μ=0.1,在金属盒内的最右端静止放置一个质量为m=2. 0kg、半径为r=0.2m的光滑金属小球,现在某时刻金属盒获得一个水平向右的初速度vo= 3m/s,不计挡板的厚度、小球与挡板碰撞的时间及能量损失,重力加速度g= l0m/s2.则:
![]()
(1)金属盒在水平桌面上运动的加速度是多少?
(2)最后系统处于静止状态时,金属小球的球心距左边档板的水平距离是多少?
【答案】(1)![]() (2)
(2)![]()
【解析】(1)金属盒受到的摩擦力f=μ(M+m)g
由牛顿第二定律:F=Ma
以上各式解得a=2m/s2
(2)金属盒与金属球第一次碰撞时,运动的距离为s1=1.4m-0.2×2m=1.0m
在这个过程中,对金属盒由动能定理:![]()
在碰撞时,动量守恒,能量守恒:![]()
![]()
解得v1′=0 v2=![]() m/s
m/s
金属球运动1m后又与挡板碰撞,碰后金属球静止,金属盒又以![]() m/s的速度运动,对金属盒由动能定理:
m/s的速度运动,对金属盒由动能定理:![]()
解得s2=1.25m大于1m,金属盒运动1m后又要与挡板碰撞,对金属盒由动能定理:![]()
解得小球第二次与金属盒碰后的速度为v2′=1m/s
对金属盒由动能定理:![]()
解得s4=0.25m
小球的球心到挡板的距离为s=1.40m-0.20m-0.25m=0.95m

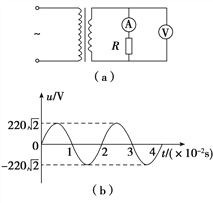
【题目】某同学设计了一个既可以测电阻由可以测电动势和内阻的实验电路,如图甲所示,实验室提供了一下实验器材:
电源E(电动势为6V,内阻约为1Ω)
定值电阻R0(阻值约为5Ω)
电流表A(量程30mA,内阻约为0.5Ω)
电流表B(量程0.6A,内阻约为1Ω)
电压表C(量程8V,内阻约为5kΩ)
电压表D(量程4V,内阻约为3kΩ)
滑动变阻器F(阻值0﹣10Ω)
滑动变阻器G(阻值0﹣500Ω)
根据题中所给信息,请回答以下问题

(1)电流表应选____,滑动变阻器应选____;(选填器材代号)
(2)该同学操作正确无误,用U1、U2、I分别表示电表V1、V2、A的读数,其数据如表所示:
I(A) | 0.30 | 0.35 | 0.40 | 0.45 | 0.50 | 0.55 |
U1(V) | 5.68 | 5.61 | 5.57 | 5.51 | 5.48 | 5.40 |
U2(V) | 1.44 | 1.69 | 1.91 | 2.16 | 2.39 | 2.62 |
根据表中数据求得定值电阻R0=_____Ω(保留两位有效数字),其测量值____真实值(填>、<或=);该同学同时利用上表测得的数据求得电源的电动势和内阻,由误差分析可知,电动势的测量值____电动势的真实值(填>、<或=).
(3)该同学进一步利用一个辅助电源E′,采用如图乙所示的电路测量电源的电动势,测量过程中,调节R后再调节R1,使得A1的示数变为0,测得多组数据,这样,电源电动势值_______电源电动势的真实值(填>、<或=).