��Ŀ����
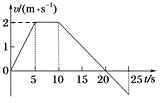
����Ŀ����ͼ��ʾ����������վ�����ȣ���һ��ֱ���ϡ�������վ��������ʻʱ�ٶȾ�Ϊ![]() ��ÿ�ο�վͣ��ʱ���Ϊt��ijͬѧ�ڳ�վ1�복վ2֮����복վ2�Ͻ���ijһλ�ã������ӳ�վ3������ͬʱ������վ2���ٶ�
��ÿ�ο�վͣ��ʱ���Ϊt��ijͬѧ�ڳ�վ1�복վ2֮����복վ2�Ͻ���ijһλ�ã������ӳ�վ3������ͬʱ������վ2���ٶ�![]() ���ٱ��ܣ���ǡ�ܸ����������������ơ����Ǹ�ͬѧ�ó����ۣ��������Դ�ƽ���ٶȴ�ԭλ����վ1���ܣ�Ҳһ���ܸϵ���������������ͨ�������ж���λͬѧ�Ľ����Ƿ���ȷ���������˽��۳����ij�λ�������������ʲô��
���ٱ��ܣ���ǡ�ܸ����������������ơ����Ǹ�ͬѧ�ó����ۣ��������Դ�ƽ���ٶȴ�ԭλ����վ1���ܣ�Ҳһ���ܸϵ���������������ͨ�������ж���λͬѧ�Ľ����Ƿ���ȷ���������˽��۳����ij�λ�������������ʲô��
![]()
���𰸡�����λ���ڳ�վ1,2���Ҳ����ֵ㼰����ࡣ
��������
������Ҫʹ�˺ͳ��ڳ�վ2���������˾վ2�ľ���Ϊx�����У�![]() ��
��
��Ҫʹ�����ڳ�վ1���ϳ������У�![]() ��
��
������ʽ�ɵã�![]() ����ֻ�е�
����ֻ�е�![]() ʱ���˲��п�����վ̨1�ϸ��ϳ���
ʱ���˲��п�����վ̨1�ϸ��ϳ���
�ʸ�ͬѧ�������Ǵ���ģ�

��ϰ��ϵ�д�
 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д� ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�
�����Ŀ