Question

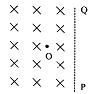
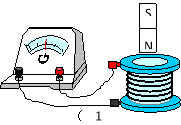
【题目】如图甲所示，两间距为d的水平放置的平行金属板M、N，M板某处C放有粒子源，C的正上方的N板D处开有一个可穿过粒子的小孔．间距L=2d的平行金属导轨P、Q与金属板M、N相连，导轨上存在一垂直纸面向里、大小为B的匀强磁场，一导体棒ab贴紧PQ以一定的初速度向右匀速进入磁场．在ab进入磁场的瞬间，粒子源飘出一个初速度视为零、质量为m、带电量为q的粒子，在M、N间加速后从D处射出．在N板的上方（并与D点相切）有一个内圆半径R1=d、外圆半径R2=3d的圆环形匀强磁场，其大小也为B、方向垂直纸面向外，两圆的圆心O与C、D在一竖直线上．不计粒子重力，忽略平行板外的电场以及磁场间的相互影响．

（1）C处飘出的粒子带何种电荷？已知ab棒的速度为v0，求粒子到达N板时速度v；

（2）为了不让粒子进入内圆半径为R1的无磁场区域，试求出ab棒的速度v0最大值v0m；

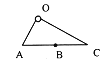
（3）若ab棒的速度只能是，为了实现粒子不进入半径为R1的内圆无磁场区域，可以控制金属导轨P、Q的磁场宽度（如图乙所示），求该磁场宽度S的范围．

Answer 1

【答案】(1)负电 (2) (3) 0＜s≤2d

【解析】试题分析：依据右手定则，从而判定粒子的电性，再依据感应电动势公式，结合动能定理，即可求解；依据题意作出最大半径的圆，再根据几何关系，结合洛伦兹力提供向心力，即可求解；为了实现粒子不进入半径为R1的内圆无磁场区域，结合运动学规律，及牛顿第二定律，从而求得磁场宽度S的范围。

（1）根据右手定则可知，a端为正极，故带电粒子必须带负电．

ab棒切割磁感线，产生的电动势为：E势=BLv0=2Bdv0

根据动能定理对于粒子有：

联立以上解得：

（2）为了不让粒子进入内圆半径为d的无磁场区域，则粒子最大半径r时的轨迹与内圆相切，如图所示．设此时粒子速度为v′

根据几何关系：

解得：r=4d

根据洛伦兹力提供向心力有：

联立解得：

根据粒子速度v与ab棒速度v0的关系式可得：

所以ab棒的速度v0的最大值为：

（3）因为，故如果让粒子一直在MN间加速，则必然进入内圆无磁场区。而如果能够让粒子在MN间只加速一部分距离，用时间t，再匀速走完剩下的距离，就可以让粒子的速度不超过v′。这时只需ab棒在磁场中运动一段距离。

设导轨磁场最大宽度为S时粒子恰好不会进入内圆无磁场区，此情况下由上可知，粒子从D点射出的速度为：

粒子在MN间加速的加速度为：

联立解得：

对于ab棒：

磁场宽度范围：0＜s≤2d