题目内容
6.1975年11月26日,我国首次成功发射返回式遥感卫星,在太空正常运行3天,取得了珍贵的对地遥感资料后,按预定计划返回地面,成为世界上继美国、前苏联之后第三个掌握卫星返回技术和空间遥感技术的国家.若此遥感探测卫星在距地球表面高度为h处绕地球转动,地球质量为M,地球半径为R,探测卫星质量为m,万有引力常量为G,试求:(1)遥感卫星的线速度;
(2)遥感卫星的运转周期.
分析 (1)卫星绕地球做圆周运动万有引力提供向心力,由万有引力公式与牛顿第二定律可以求出线速度.
(2)卫星绕地球做圆周运动万有引力提供向心力,由万有引力公式与牛顿第二定律可以求出周期.
解答 解:(1)万有引力提供向心力,由牛顿第二定律得:
G$\frac{Mm}{(R+h)^{2}}$=m$\frac{{v}^{2}}{R+h}$,
解得线速度:v=$\sqrt{\frac{GM}{R+h}}$;
(2)万有引力提供向心力,由牛顿第二定律得:
G$\frac{Mm}{(R+h)^{2}}$=m$(\frac{2π}{T})^{2}$(R+h),
解得周期:T=2π$\sqrt{\frac{(R+h)^{3}}{GM}}$;
答:(1)遥感卫星的线速度为$\sqrt{\frac{GM}{R+h}}$;
(2)遥感卫星的运转周期为2π$\sqrt{\frac{(R+h)^{3}}{GM}}$.
点评 本题考查了万有引力定律的应用,知道万有引力提供向心力是解题的前提,应用万有引力公式与牛顿第二定律可以解题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
17.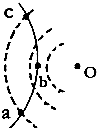 一带电粒子射入一固定在O点的点电荷的电场中,粒子运动轨迹如图中实线abc所示.图中虚线是同心圆弧,表示电场的等势面.不计重力,可以判断( )
一带电粒子射入一固定在O点的点电荷的电场中,粒子运动轨迹如图中实线abc所示.图中虚线是同心圆弧,表示电场的等势面.不计重力,可以判断( )
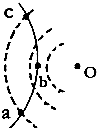 一带电粒子射入一固定在O点的点电荷的电场中,粒子运动轨迹如图中实线abc所示.图中虚线是同心圆弧,表示电场的等势面.不计重力,可以判断( )
一带电粒子射入一固定在O点的点电荷的电场中,粒子运动轨迹如图中实线abc所示.图中虚线是同心圆弧,表示电场的等势面.不计重力,可以判断( )| A. | 此粒子一直受到静电吸引力作用 | |
| B. | 粒子在b点的电势能一定大于在a点的电势能 | |
| C. | 粒子在a 点和c点的速度相同 | |
| D. | 粒子在b 点的速度一定大于在a 点的速度 |
14.关于斜抛运动的性质以下说法正确的是( )
| A. | 斜抛运动是匀变速运动,因为其速度是恒定的 | |
| B. | 斜抛运动是匀变速运动,因为其加速度是恒定的 | |
| C. | 斜抛运动是非匀变速运动,因为其速度是变化的 | |
| D. | 斜抛运动是非匀变速运动,因为其加速度是变化的 |
18.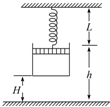 如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),当温度升高时,改变的量有( )
如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),当温度升高时,改变的量有( )
 如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),当温度升高时,改变的量有( )
如图所示,一导热性良好的汽缸内用活塞封住一定量的气体(不计活塞与缸壁摩擦),当温度升高时,改变的量有( )| A. | 活塞高度h | B. | 汽缸底距地面高度H | ||
| C. | 气体压强p | D. | 弹簧长度L |
16.某导体中的电流随其两端电压的变化如图所示,下列说法正确的是( )
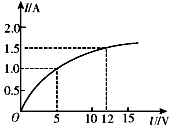

| A. | 加5 V电压时,导体的电阻约是5Ω | |
| B. | 加12 V电压时,导体的电阻约是1.4Ω | |
| C. | 由图可知随着电压的增大,导体的电阻不断减小 | |
| D. | 由图可知随着电压的减小,导体的电阻不断减小 |
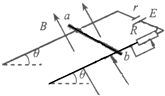 如图所示,在倾角为30°的斜面上,固定一宽度为L=0.25m的足够长平行光滑金属导轨,在导轨上端接入电源和滑动变阻器.电源电动势为E=1.5V,内阻为r=0.6Ω.一质量m=20g的金属棒ab与两导轨垂直并接触良好.整个装置处于垂直于斜面向上的匀强磁场中,磁感应强度为B=0.80T.导轨与金属棒的电阻不计,取g=10m/s2.
如图所示,在倾角为30°的斜面上,固定一宽度为L=0.25m的足够长平行光滑金属导轨,在导轨上端接入电源和滑动变阻器.电源电动势为E=1.5V,内阻为r=0.6Ω.一质量m=20g的金属棒ab与两导轨垂直并接触良好.整个装置处于垂直于斜面向上的匀强磁场中,磁感应强度为B=0.80T.导轨与金属棒的电阻不计,取g=10m/s2. 如图所示,在距一质量为m0、半径为R、密度均匀的大球体R处有一质量为m的质点,此时大球体对质点的万有引力为F1,当从大球体中挖去一半径为$\frac{R}{2}$的小球体后(空腔的表面与大球体表面相切),剩下部分对质点的万有引力为F2,求F1:F2.
如图所示,在距一质量为m0、半径为R、密度均匀的大球体R处有一质量为m的质点,此时大球体对质点的万有引力为F1,当从大球体中挖去一半径为$\frac{R}{2}$的小球体后(空腔的表面与大球体表面相切),剩下部分对质点的万有引力为F2,求F1:F2.