题目内容
14.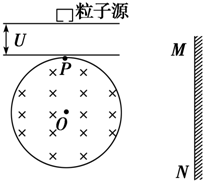 如图所示,在半径为R的圆形区域内有水平向里的匀强磁场,圆形区域右侧距离圆形区域右边缘为d处有一竖直感光板.圆形区域上侧有两块平行金属极板,金属极板上侧有一粒子源,粒子源中可以发射速度很小的质量为m的2价阳离子(带电量为+2e),离子重力不计.
如图所示,在半径为R的圆形区域内有水平向里的匀强磁场,圆形区域右侧距离圆形区域右边缘为d处有一竖直感光板.圆形区域上侧有两块平行金属极板,金属极板上侧有一粒子源,粒子源中可以发射速度很小的质量为m的2价阳离子(带电量为+2e),离子重力不计.(1)若离子从圆形区域顶点P以速率v0平行于纸面进入磁场,求在两块平行金属极板上所加的电压U;
(2)若离子从圆形区域顶点P以速率v0对准圆心射入,若它刚好从圆形区域最右侧射出,垂直打在竖直感光板上,求圆形区域内磁场的磁感应强度B;
(3)若圆形区域内的磁场的磁感应强度为B,离子以某一速度对准圆心射入,若它从圆形区域右侧射出,以与竖直感光板成60°的角打在竖直感光板上,求它打到感光板上时的速度;
(4)若在圆形区域右侧加上竖直向下的匀强电场,电场强度为E,粒子从圆弧顶点P以速率v0对准圆心射入,求离子打在MN上的位置距离圆形区域圆心O的竖直高度h.
分析 (1)离子在金属极板间做匀加速运动,由动能定理求解电压U.
(2)离子进入磁场后做匀速圆周运动,若离子从圆形区域顶点P对准圆心射入,刚好从圆形区域最右侧射出时,其在磁场中运动轨迹为$\frac{1}{4}$圆弧,画出轨迹,求出轨迹半径,由牛顿第二定律求解磁感应强度.
(3)结合题意画出离子的运动轨迹,由几何知识求出轨迹半径,即可求得离子的速度.
(4)离子从Q点射出后做类平抛运动,运用运动的分解,由牛顿第二定律和位移公式结合解答.
解答 解:(1)由动能定理可知,2eU=$\frac{1}{2}$mv02
解得 U=$\frac{m{{v}_{0}}^{2}}{4e}$.
(2)设离子进入磁场中做匀速圆周运动的轨道半径为r,根据题述,离子在磁场中的运动轨迹为四分之一圆周,且r=R,如图甲所示,由牛顿第二定律得:
2ev0B=m$\frac{{{v}_{0}}^{2}}{r}$
解得:B=$\frac{m{v}_{0}}{2eR}$ 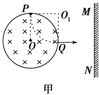
(3)根据题述可知离子以与竖直感光板成60°的角打在竖直感光板上,离子轨迹如图乙所示.由图中几何关系可知,tan60°=$\frac{r}{R}$ 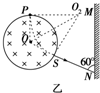
解得离子轨迹半径r=$\sqrt{3}$R
由2evB=m$\frac{{v}^{2}}{r}$,解得:v=$\frac{2\sqrt{3}eBR}{m}$.
(4)离子从Q点射出后做类平抛运动,如图丙所示,且
d=v0t,h=$\frac{1}{2}$at2(2分)
由牛顿第二定律有 a=$\frac{2eE}{m}$
联立解得:h=$\frac{eE{d}^{2}}{m{v}_{0}^{2}}$. 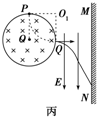
答:
(1)在两块平行金属极板上所加的电压U为$\frac{m{{v}_{0}}^{2}}{4e}$.
(2)圆形区域内磁场的磁感应强度B为$\frac{m{v}_{0}}{2eR}$.
(3)它打到感光板上时的速度为$\frac{2\sqrt{3}eBR}{m}$.
(4)离子打在MN上的位置距离圆形区域圆心O的竖直高度h为$\frac{eE{d}^{2}}{m{v}_{0}^{2}}$.
点评 本题考查带电粒子在磁场中的运动,掌握带电粒子在磁场中运动的半径公式.本题对数学几何能力要求较高,需加强这方面的训练.

| A. | 月球绕地球运动的周期T1及月球到地球中心的距离R1 | |
| B. | 地球绕太阳运行周期T2及地球到太阳中心的距离R2 | |
| C. | 人造卫星的质量和它在地面附近的运行速度v3 | |
| D. | 地球绕太阳运行的速度v4及地球到太阳中心的距离R4 |
 如图,蹲在树枝上的一只松鼠看到一个猎人正在用枪水平瞄准它,就在子弹出枪口时,开始逃跑,松鼠可能的逃跑方式有
如图,蹲在树枝上的一只松鼠看到一个猎人正在用枪水平瞄准它,就在子弹出枪口时,开始逃跑,松鼠可能的逃跑方式有①自由落下;
②竖直上跳;
③背着枪口,沿AC方向水平跳离树枝;
④迎着枪口,沿AB方向水平跳离树枝.
在这四种逃跑方式中,松鼠不能逃脱厄运而被击中的是(设树枝足够高)( )
| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②④ |
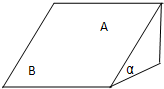 如图所示,一质量为m的滑块从斜面(固定在水平地面上)的A点做曲线运动到B点,经过的路程为S,位移为L,AB两点的竖直高度差为H,设整个过程中滑动摩擦力的大小恒为f,则下列说法正确的是( )
如图所示,一质量为m的滑块从斜面(固定在水平地面上)的A点做曲线运动到B点,经过的路程为S,位移为L,AB两点的竖直高度差为H,设整个过程中滑动摩擦力的大小恒为f,则下列说法正确的是( )| A. | 滑块从A到B过程中,重力做功为mgH | |
| B. | 滑块从A到B过程中,滑动摩擦力做功为-fL | |
| C. | 滑块从A到B过程中,滑动摩擦力做功为-fS | |
| D. | 斜面对滑块的支持力不做功 |
| A. | 10m/s | B. | 14.1m/s | C. | 12.6m/s | D. | 4m/s |
| A. | 向下,m(v1-v2) | B. | 向下,m(v1+v2) | C. | 向上,m(v1-v2) | D. | 向上,m(v1+v2) |
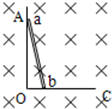 如图所示,立在导轨上的ab金属直棒,从静止开始在重力作用下运动,在运动过程中,b端始终在OC上,a端始终在AO上,直到ab棒完全落在OC上.空间存在着方向垂直纸面向里的匀强磁场,则ab棒在运动过程中流过ab棒的感应电流方向( )
如图所示,立在导轨上的ab金属直棒,从静止开始在重力作用下运动,在运动过程中,b端始终在OC上,a端始终在AO上,直到ab棒完全落在OC上.空间存在着方向垂直纸面向里的匀强磁场,则ab棒在运动过程中流过ab棒的感应电流方向( )| A. | 始终是a→b | B. | 始终是b→a | ||
| C. | 先是a→b,后变为b→a | D. | 先是b→a,后变为a→b |
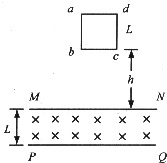 如图所示,在高度为L=1m、足够宽的区域MNPQ内,有垂直纸面向里的匀强磁场,磁感应强度为B=1T.质量为m=1kg、边长为L=1m、总电阻R=1Ω的正方形导线框abcd(线框每条边的电阻相同),在MN上方某一高度由静止开始自由下落.当bc边进入磁场时,导线框恰好做匀速运动.已知重力加速度为g取10m/s2,不计空气阻力,求:
如图所示,在高度为L=1m、足够宽的区域MNPQ内,有垂直纸面向里的匀强磁场,磁感应强度为B=1T.质量为m=1kg、边长为L=1m、总电阻R=1Ω的正方形导线框abcd(线框每条边的电阻相同),在MN上方某一高度由静止开始自由下落.当bc边进入磁场时,导线框恰好做匀速运动.已知重力加速度为g取10m/s2,不计空气阻力,求: