题目内容
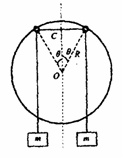
如题图所示,abc是光滑的轨道,其中ab是水平的,bc为与ab相切的位于竖直平面内的半圆,半径R=0.30m。质量m=0.20kg的小球A静止在轨道上,另一质量M=0.60kg、速度V0=5.5m/s的小球B与小球A正碰。已知相碰后小球A经过半圆的最高点c落到轨道上距b点为L="4"  R处,重力加速度g取10m/s2,求:
R处,重力加速度g取10m/s2,求:

(1)碰撞结束时,小球A和B的速度大小;
(2)试论证小球B是否能沿着半圆轨道到达c点?
 R处,重力加速度g取10m/s2,求:
R处,重力加速度g取10m/s2,求:
(1)碰撞结束时,小球A和B的速度大小;
(2)试论证小球B是否能沿着半圆轨道到达c点?
(1)v1="6m/s" , v2="3.5m/s. " (2)vB=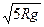 =3.9m/s>v2,可知小球B不能达到半圆轨道的最高点。
=3.9m/s>v2,可知小球B不能达到半圆轨道的最高点。
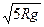 =3.9m/s>v2,可知小球B不能达到半圆轨道的最高点。
=3.9m/s>v2,可知小球B不能达到半圆轨道的最高点。(1)分别以v1和v2表示小球A和B碰后的速度,v3表示小球A在半圆最高点的速度,则对A由平抛运动规律有:L=v3t 和 h=2R=gt2/2
解得: v3=2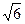 m/s.
m/s.
对A运用机械能守恒定律得:mv12/2=2mgR+mv32/2
以A和B为系统,碰撞前后动量守恒:Mv0=Mv2+mv1
联立解得:v1="6m/s" , v2="3.5m/s. "
(2)小球B刚能沿着半圆轨道上升到最高点的条件是在最高点弹力为零、重力作为向心力,故有:Mg=mvc2/R
由机械能守恒定律有:MVB2/2=2RMg+Mvc2/2
解得:vB=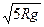 =3.9m/s>v2,可知小球B不能达到半圆轨道的最高点。
=3.9m/s>v2,可知小球B不能达到半圆轨道的最高点。
解得: v3=2
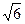 m/s.
m/s. 对A运用机械能守恒定律得:mv12/2=2mgR+mv32/2
以A和B为系统,碰撞前后动量守恒:Mv0=Mv2+mv1
联立解得:v1="6m/s" , v2="3.5m/s. "
(2)小球B刚能沿着半圆轨道上升到最高点的条件是在最高点弹力为零、重力作为向心力,故有:Mg=mvc2/R
由机械能守恒定律有:MVB2/2=2RMg+Mvc2/2
解得:vB=
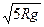 =3.9m/s>v2,可知小球B不能达到半圆轨道的最高点。
=3.9m/s>v2,可知小球B不能达到半圆轨道的最高点。
练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目

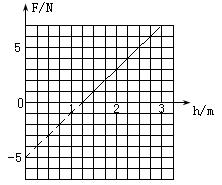
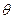 ,高为h,有一质量为m的物体从斜面顶端由静止开始滑到底端,求:
,高为h,有一质量为m的物体从斜面顶端由静止开始滑到底端,求:
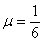 , 轨道其余各部分的表面光滑.一个质量为m="2" kg的滑环(套在滑轨上),从AB的中点E处以v0="10" m/s的初速度水平向右运动.已知
, 轨道其余各部分的表面光滑.一个质量为m="2" kg的滑环(套在滑轨上),从AB的中点E处以v0="10" m/s的初速度水平向右运动.已知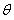 =37°(g取10 m/s2) 试求:
=37°(g取10 m/s2) 试求: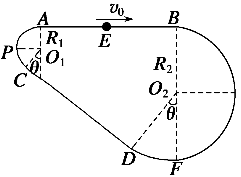
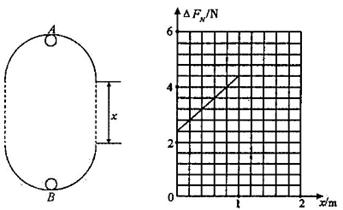
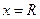 时,为使小球不脱离轨道运动,求小球在B点的最小速度(用物理量的符号表示)
时,为使小球不脱离轨道运动,求小球在B点的最小速度(用物理量的符号表示)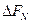 与
与 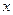 的函数关系。(用
的函数关系。(用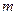 、
、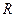 、
、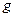 表示)
表示)
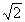 m的重物,使两个小圆环间的绳子水平,然后无初速释放重物M.设绳子与大、小圆环间的摩擦均可忽略,求重物M下降的最大距离.
m的重物,使两个小圆环间的绳子水平,然后无初速释放重物M.设绳子与大、小圆环间的摩擦均可忽略,求重物M下降的最大距离.