题目内容
【题目】有一金属细棒ab,质量m=0.05kg,电阻不计,可在两条轨道上滑动,如图所示,轨道间距为L=0.5m,其平面与水平面的夹角为θ=37°,置于垂直于轨道平面向上的匀强磁场中,磁感应强度为B=1.0T,金属棒与轨道的动摩擦因数μ=0.5,(设最大静摩擦力与滑动摩擦力大小相等)回路中电源电动势为E=3V,内阻r=0.5Ω.(g=10m/s2,sin37°=0.6,cos37°=0.8)求:
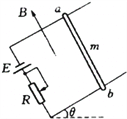
①为保证金属细棒不会沿斜面向上滑动,流过金属细棒ab的电流的最大值为多少?
②滑动变阻器R的阻值应调节在什么范围内,金属棒能静止在轨道上?
【答案】(1) ![]() (2)2.5Ω≤R≤14.5Ω
(2)2.5Ω≤R≤14.5Ω
【解析】(1)当金属棒正要向上滑动时,摩擦力沿斜面向下并达最大,此时通过金属棒的电流达到最大I1,由平衡条件得:mgsinθ+μmgcosθ=BLI1
代入数据解得:I1=1A
(2)由![]() ,代入数据解得:R1=2.5Ω
,代入数据解得:R1=2.5Ω
当金属棒正要向下滑动时,摩擦力沿斜面向上并达最大,此时通过金属棒的电流最小为I2,
由平衡条件得:mgsinθ=μmgcosθ+BLI2
由闭合电路欧姆定律得: ![]() ,解得:R2=14.5Ω,
,解得:R2=14.5Ω,
因此滑动变阻器的阻值范围是:2.5Ω≤R≤14.5Ω;

【题目】某同学在探究 “加速度与力、质量的关系”实验中探究加速度与力的关系,在保持小车质量不变的情况下,测得小车的加速度a和拉力F的数据如下表所示

F/N | 0.21 | 0.30 | 0.40 | 0.49 |
a /m·s-2 | 0.10 | 0.21 | 0.29 | 0.41 |
①根据测量的数据,在图中作a-F图象;
② 图线在F轴截距的物理意义是_____;
③ 应如何调整实验装置,才能使作出的
a-F图线过坐标原点____。(填标号)
A.增加小车的质量 B.减小小车的质量
C.适当增大长木板的倾角 D.适当减小小桶内钩码质量