Question

【题目】如图（a），某同学骑自行车以速率v1进入一段直下坡，在坡道上不蹬踏板而自由加速下滑。自行车受到路面的阻力略去不计，空气阻f1与车速大小成正比，比例系数为k，方向与车速方向相反，人与车总质量为m，重力加速度为g．已知自行车到坡底时的速率为v2．

（1）在图（b）中定性画出自行车在坡道上的速率v与在坡道上运动时间t1的关系；

（2）到坡底以速率v2进入平直路面后，该同学立即开始刹车。在刹车阻力f2和空气阻力f1的共同作用下匀减速运动T时间后停止，求刹车阻力f2与刹车时间t2的关系，以及刹车过程f2的冲量；

（3）在第（2）问中，已知刹车过程前轮与地面接触处始终不打滑。从开始刹车时测量，车载速率表显示前轮转动第一圈过程车辆前进的平均速度为7.0m/s，转动第二圈过程车辆前进的平均速度为6.0m/s，则该刹车过程前轮总共转了多少圈（解出数值结果，保留一位小数）？

Answer 1

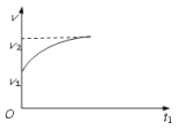
【答案】（1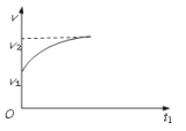）（2）；；（3）4.1

【解析】

（1）车在坡道上下行时加速度为，则随着速度的增加，加速度减小，则速度-时间图像大致为：

（2）刹车后做匀减速运动，则加速度为

则任意时刻t2的速度

则由牛顿第二定律

联立解得

则f2-t2关系为线性关系，画出f2-t2图像，则图像与坐标轴围成的面积等于f2的冲量。

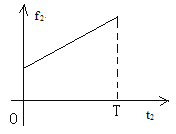
（3）设车轮周长为L，车做匀减速运动的加速度为a，刚刹车时的初速度为v，则车轮转过第一圈时的速度v1满足，即

v1=14-v；

同理车轮转过第二圈时的速度

v2=v-2

则

联立解得：

则

联立解得

则该刹车过程前轮总共转了4.1圈.