题目内容
（2009?海淀区一模）设质量相等的甲、乙两颗卫星，分别贴近某星球表面和地球表面，环绕其球心做匀速圆周运动，已知该星球和地球的密度相同，其半径分别为R和r，则（ ）
分析：根据万有引力提供向心力，可分别得出卫星周期、线速度、向心力、向心加速度与半径关系表达式，进行分析求解．
解答：解：A、万有引力分别提供两者的向心力，即
=man，故an=
=
=
Gπr，故甲、乙两颗卫星的加速度之比等于R：r，故A正确
B、由Fn=man，结合A分析得，B错误
C、由于an=
，所以v=
，结合A的分析知，线速度之比为R：r，故C错误
D、由线速度公式v=
，结合C分析知，甲、乙两颗卫星的周期之比等于1：1，故D错误
故选A
| GMm |
| r2 |
| GM |
| r2 |
G
| ||
| r2 |
| 4 |
| 3 |
B、由Fn=man，结合A分析得，B错误
C、由于an=
| v2 |
| r |
| anr |
D、由线速度公式v=
| 2πr |
| T |
故选A
点评：对于人造地球卫星问题，常常建立这样模型：卫星绕地球做匀速圆周运动，地球对卫星的万有引力提供卫星的向心力，由于运算量较大，给学生带来一定的难度．
练习册系列答案
相关题目
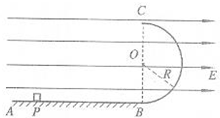（2009?海淀区一模）如图所示，水平绝缘轨道AB与处于竖直平面内的半圆形绝缘光滑轨道BC平滑连接，半圆形轨道的半径R=0.40m．轨道所在空间存在水平向右的匀强电场，电场强度E=1.0×104N/C．现有一电荷量q=+1.0×10-4C，质量m=0.10kg的带电体（可视为质点），在水平轨道上的P点由静止释放，带电体运动到圆形轨道最低点B时的速度vB=5.0m/s．已知带电体与水平轨道间的动摩擦因数μ=0.50，重力加速度g=10m/s2．求：
（2009?海淀区二模）为估测一照相机的曝光时间，实验者从某砖墙前的高处使一个石子自由落下，拍摄石子在空中的照片如图所示．由于石子的运动，它在照片上留下了一条模糊的径迹．已知每层砖的平均厚度为6cm，拍摄到的石子位置A 距石子起落点竖直距离约5m．这个照相机的曝光时间约为（ ）