题目内容

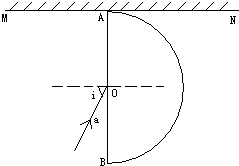
如图所示，AOB为半圆形玻璃砖截面，玻璃的折射率为n=
2
现有一束平行光线以45°角入射到 AB面上后，经折射从半圆面上的部分位置射出．试求半圆柱面能被照亮的部分与整个半圆柱面的面积之比．
根据折射定律得，
sin45°
sinθ
=n
光在AB面上的折射角θ=30°．
在曲面上发生全反射的临界角sinC=
1
2
，得C=45°
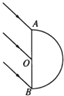
如图根据几何关系得，E点以上和F点以下的光线发生全反射，不能从曲面上射出，有光线射出的部分为EF部分．
根据几何关系解得，∠AOE=75°，∠BOF=15°，所以∠EOF=90°．
故被照亮的面积与整个半圆柱的面积之比为1：2
答：半圆柱面能被照亮的部分与整个半圆柱面的面积之比为1：2．
练习册系列答案
相关题目
（8分）【物理－物理3-4】

（1）（3分）湖面上漂着A、B两片小树叶，它们相距27m。一列水波（可看作简谐横波）正在湖面上传播，每片小树叶每分钟上下浮动20次。当A树叶位于波峰时，B树叶在波谷，两树叶之间还有一个波峰。则水波的波速为           
（2）（5分）如图所示，为用某种透明材料制成的一块长方体棱镜的截面图，O为BC的中心，光线从AB面入射，入射角为60°，光线进入棱镜后射在O点并恰好不从BC面射出．已知真空中的光速．
①画出光线从开始射入棱镜到射出棱镜后的完整光路图。
②求该棱镜的折射率和光线在棱镜中传播速度的大小（结果可保留根号）。
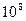光在某种介质中的传播速度为1.5×m/s,则光从此介质射向真空的临界角是             .
用如图所示的装置可以测定玻璃的折射率．在光具盘上固定一块半圆柱形新型玻璃砖，使二者的圆心重合．让激光束从玻璃砖圆弧面一侧射入，光束垂直玻璃砖底面并通过圆心O．保持入射光束方向不变，以圆心为轴逆时针方向缓慢转动光具盘，同时发现有两束光在光具盘上移动，当光具盘转过θ=30°角时，发现其中一束光恰好消失，求新型玻璃砖的折射率n=______．
（1）如图甲所示，一列简谐波沿x轴传播，实线为t=0时的波形图，此时P质点向y轴负方向运动，虚线为经过0.01s时第一次出现的波形图，则波沿x轴______（填“正”或“负”）方向传播，波速为______m/s．
（2）某同学欲测直角三棱镜ABC的折射率n．他让光线沿平行于BC边的方向射到三棱镜的侧面AB上，经棱镜AB边和AC边的两次折射和BC边的一次反射后，又从另一侧面AC边上的P点射出．
①在图乙上画出光路图；
②若将射向AB边的光的入射角调整为α=60°，此时的折射角γ=30°，求折射率n的值．
如图是一个透明圆柱介质的横截面，B、C为圆上两点．一束单色光沿AB方向入射，从c点射出，已知∠ABO=∠BOC=120°，真空中光速c=3×108m/s．求：
①光在介质中的折射率n
②光在介质中传播速度v．
让光线通过一块两面平行的玻璃砖，下列判断中错误的是（　　）
A．出射光线的方向与平行玻璃砖的厚度有关
B．出射光线的方向与玻璃的折射率有关，n越大偏向角越大
C．光线通过玻璃砖后发生侧向移动而方向不变
D．光线通过玻璃砖，射出玻璃砖时不可能发生全反射
如图所示，半圆圆玻璃砖的半径R=10cm，折射率n=
3
，直径AB与屏幕MN垂直并接触于A点，激光a以入射角i=60射向玻璃砖圆心O，结果在屏幕MN上出现两光斑，求：
（1）射入玻璃光线的折射角；
（2）画出形成两光斑的光路；
（3）两光斑之间的距离L．
如图所示，画有直角坐标系xOy的白纸位于水平桌面上，M是放在白纸上的半圆玻璃砖，其底面的圆心在坐标系原点，直边与x轴重合，OA是画在纸上的直线，P1、P2为竖直的插在直线OA上的两枚大头针，P3是竖直插在纸上的第三枚大头针，α是直线OA与y轴正方向的夹角，β是直线OP3与y轴负方向的夹角，只要直线OA画得合适，且P3的位置取得正确，测得角α、β便可求得玻璃的折射率．某学生在用上述方法测量玻璃的折射率时，在他画出的直线OA上竖直插上了P1、P2两枚大头针，但在y＜0的区域内，不管眼睛放在何处，都无法透过玻璃看到P1、P2的像，他应采取的措施是______．若他已正确地测得了α、β的值，则玻璃的折射率n=______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网