题目内容
【题目】如图(a)所示，“
”型木块放在光滑水平地面上，木块水平表面AB粗糙，斜面BC光滑且与水平面夹角为θ=37°.木块右侧与竖直墙壁之间连接着一个力传感器，当力传感器受压时，其示数为正值；当力传感器被拉时，其示数为负值．一个可视为质点的滑块从C点由静止开始下滑，运动过程中，传感器记录到的力和时间的关系如图(b)所示．已知sin 37°=0.6，cos 37°=0.8，g取10 m/s2.求：
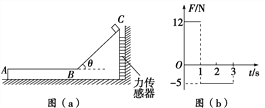
(1)斜面BC的长度；
(2)滑块与木块水平表面AB的摩擦因数．
【答案】(1)3 m(2)0.2
【解析】试题分析：根据牛顿第二定律求出滑块在斜面上运动的加速度，结合位移时间公式求出滑块的位移．根据木板对传感器的压力得出物块的质量，结合传感器对木板的拉力求出滑动摩擦力的大小，结合滑动摩擦力公式求出动摩擦因数的大小．
（1）分析滑块受力，由牛顿第二定律得：
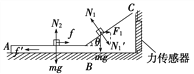
得： 
，
通过图象可知滑块在斜面上运动的时间为： 
由运动学公式得
.
（2）滑块对斜面的压力为： 
，木块对传感器的压力为： 
，由图象可知： 
．解得： 
.传感器对木块的拉力
，则
.
练习册系列答案
名校课堂系列答案
相关题目
