题目内容
15. 一质量为m的小球栓在细绳的一端,另一端大小为F的拉力作用,在水平面上做半径为R的匀速圆周运动,如图所示,现将拉力逐渐增大,当拉力增大到8F时,小球仍做匀速圆周运动,半径为$\frac{R}{2}$.试求该过程中拉力所做的功.
一质量为m的小球栓在细绳的一端,另一端大小为F的拉力作用,在水平面上做半径为R的匀速圆周运动,如图所示,现将拉力逐渐增大,当拉力增大到8F时,小球仍做匀速圆周运动,半径为$\frac{R}{2}$.试求该过程中拉力所做的功.
分析 物体在光滑水平面上做匀速圆周运动,由绳子的拉力提供向心力,根据牛顿第二定律分别求出两种拉力情况下物体的速度,再根据动能定理求出拉力对物体所做的功.
解答 解:设当绳的拉力为F时,小球做匀速圆周运动的线速度为v1,则有 F=m$\frac{{v}_{1}^{2}}{R}$.
当绳的拉力增大到8F时,设小球做匀速圆周运动的线速度为v2,则有 8F=m$\frac{{v}_{2}^{2}}{\frac{R}{2}}$.
在绳的拉力由F增至为8F的过程中,根据动能定理得
W=$\frac{1}{2}$mv22-$\frac{1}{2}$mv12
联立解得 W=$\frac{3}{2}$FR.
答:该过程中拉力所做的功为$\frac{3}{2}$FR.
点评 本题是向心力与动能定理的综合应用,要明确它们之间的纽带是速度.

练习册系列答案
相关题目
5. 如图所示,竖直平面内放一直角杆AOB,杆的水平部分粗糙,动摩擦因数μ=0.2,杆的竖直部分光滑.两部分各套有质量均为1kg的小球A和B,A、B球间用细绳相连.初始A、B均处于静止状态,已知:OA=3m,OB=4m.若A球在水平拉力F的作用下向右缓慢地移动1m(取g=10m/s2),那么该过程中拉力F做功为( )
如图所示,竖直平面内放一直角杆AOB,杆的水平部分粗糙,动摩擦因数μ=0.2,杆的竖直部分光滑.两部分各套有质量均为1kg的小球A和B,A、B球间用细绳相连.初始A、B均处于静止状态,已知:OA=3m,OB=4m.若A球在水平拉力F的作用下向右缓慢地移动1m(取g=10m/s2),那么该过程中拉力F做功为( )
 如图所示,竖直平面内放一直角杆AOB,杆的水平部分粗糙,动摩擦因数μ=0.2,杆的竖直部分光滑.两部分各套有质量均为1kg的小球A和B,A、B球间用细绳相连.初始A、B均处于静止状态,已知:OA=3m,OB=4m.若A球在水平拉力F的作用下向右缓慢地移动1m(取g=10m/s2),那么该过程中拉力F做功为( )
如图所示,竖直平面内放一直角杆AOB,杆的水平部分粗糙,动摩擦因数μ=0.2,杆的竖直部分光滑.两部分各套有质量均为1kg的小球A和B,A、B球间用细绳相连.初始A、B均处于静止状态,已知:OA=3m,OB=4m.若A球在水平拉力F的作用下向右缓慢地移动1m(取g=10m/s2),那么该过程中拉力F做功为( )| A. | 14J | B. | 10J | C. | 6J | D. | 4J |
6.NA表示阿伏伽德罗常数,下列判断正确的是( )
| A. | 在18gO2中含有NA个氧原子 | |
| B. | 标准状况下,22.4L空气含有NA个单质分子 | |
| C. | 1 molCl2参加反应转移电子数一定为2NA | |
| D. | 1.7g H2O2中含有的电子数为0.9 NA |
3.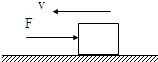 如图所示,质量m=10kg的物体在水平面上向左运动,物体与水平面间的动摩擦因数为0.2,与此同时物体受到一个水平向右的推力F=20N的作用,g取为10m/s2,则物体产生的加速度是( )
如图所示,质量m=10kg的物体在水平面上向左运动,物体与水平面间的动摩擦因数为0.2,与此同时物体受到一个水平向右的推力F=20N的作用,g取为10m/s2,则物体产生的加速度是( )
 如图所示,质量m=10kg的物体在水平面上向左运动,物体与水平面间的动摩擦因数为0.2,与此同时物体受到一个水平向右的推力F=20N的作用,g取为10m/s2,则物体产生的加速度是( )
如图所示,质量m=10kg的物体在水平面上向左运动,物体与水平面间的动摩擦因数为0.2,与此同时物体受到一个水平向右的推力F=20N的作用,g取为10m/s2,则物体产生的加速度是( )| A. | 0 | B. | 4m/s2,水平向右 | C. | 2m/s2,水平向左 | D. | 2m/s2,水平向右 |
10. 如图所示,两束不同的单色细光束a、b,以不同的入射角从空气射入玻璃三棱镜中,其出射光恰好合为一束,以下判断正确的是( )
如图所示,两束不同的单色细光束a、b,以不同的入射角从空气射入玻璃三棱镜中,其出射光恰好合为一束,以下判断正确的是( )
 如图所示,两束不同的单色细光束a、b,以不同的入射角从空气射入玻璃三棱镜中,其出射光恰好合为一束,以下判断正确的是( )
如图所示,两束不同的单色细光束a、b,以不同的入射角从空气射入玻璃三棱镜中,其出射光恰好合为一束,以下判断正确的是( )| A. | 在同种介质中b光的速度较大 | |
| B. | 该玻璃三棱镜对a 光的折射率较小 | |
| C. | 若让a、b光分别照射同种金属,都能发生光电效应,则b光照射金属产生光电子的最大初动能较大 | |
| D. | 若让a、b光分别通过同一双缝装置,在同位置的屏上形成干涉图样,则b光条纹间距较大 |
20. 如图所示,在水平面上叠放着的两个物体A,B在水平外力F的作用下向右做匀加速运动(A,B保持相对静止),设A与B间的摩擦因数为μ1,B与地面间的动摩擦因数为μ2,则关于这两个动摩擦因数μ1,μ2的说法可能正确的是( )
如图所示,在水平面上叠放着的两个物体A,B在水平外力F的作用下向右做匀加速运动(A,B保持相对静止),设A与B间的摩擦因数为μ1,B与地面间的动摩擦因数为μ2,则关于这两个动摩擦因数μ1,μ2的说法可能正确的是( )
 如图所示,在水平面上叠放着的两个物体A,B在水平外力F的作用下向右做匀加速运动(A,B保持相对静止),设A与B间的摩擦因数为μ1,B与地面间的动摩擦因数为μ2,则关于这两个动摩擦因数μ1,μ2的说法可能正确的是( )
如图所示,在水平面上叠放着的两个物体A,B在水平外力F的作用下向右做匀加速运动(A,B保持相对静止),设A与B间的摩擦因数为μ1,B与地面间的动摩擦因数为μ2,则关于这两个动摩擦因数μ1,μ2的说法可能正确的是( )| A. | μ1=0,μ2=0 | B. | μ1=0,μ2≠0 | C. | μ1≠0,μ2=0 | D. | μ1≠0,μ2≠0 |
7. 如图所示区域内存在匀强磁场,磁场的边界是一上底边和高均为L的等腰梯形,现把一边长也为L的正方形单匝线框以水平速度v水平匀速地拉过该磁场区,磁场区的磁感应强度为B,线框电阻R,零时刻线框进入磁场,不计一切摩擦阻力,则( )
如图所示区域内存在匀强磁场,磁场的边界是一上底边和高均为L的等腰梯形,现把一边长也为L的正方形单匝线框以水平速度v水平匀速地拉过该磁场区,磁场区的磁感应强度为B,线框电阻R,零时刻线框进入磁场,不计一切摩擦阻力,则( )
 如图所示区域内存在匀强磁场,磁场的边界是一上底边和高均为L的等腰梯形,现把一边长也为L的正方形单匝线框以水平速度v水平匀速地拉过该磁场区,磁场区的磁感应强度为B,线框电阻R,零时刻线框进入磁场,不计一切摩擦阻力,则( )
如图所示区域内存在匀强磁场,磁场的边界是一上底边和高均为L的等腰梯形,现把一边长也为L的正方形单匝线框以水平速度v水平匀速地拉过该磁场区,磁场区的磁感应强度为B,线框电阻R,零时刻线框进入磁场,不计一切摩擦阻力,则( )| A. | 当t=$\frac{L}{v}$时,水平拉力有最大值为$\frac{{B}^{2}{L}^{2}v}{R}$ | |
| B. | 当t=$\frac{2L}{v}$时,水平拉力有最大功率为$\frac{{B}^{2}{L}^{2}{v}^{2}}{R}$ | |
| C. | 在0~$\frac{L}{v}$时间内,水平拉力做功为$\frac{{B}^{2}{L}^{3}v}{2R}$ | |
| D. | 在0~$\frac{L}{v}$和$\frac{L}{v}$~$\frac{2L}{v}$两段时间内水平拉力做功相同 |
18.质量分别为m1和m2的两个物体,m1>m2,在两个力F1和F2作用下沿力的方向移动了相同距离.若F1做的功为W1,F2做的功为W2,则( )
| A. | W1>W2 | B. | W1<W2 | C. | W1=W2 | D. | 无法确定 |
 如图为一理想变压器,ab为原线圈,ce为副线圈,d为副线圈引出的一个接头.变压器的原线圈两端所加的正弦式交变电压的最大值Um=400V.若只在ce间接一只Rce=400Ω的电阻,或只在de间接一只Rde=225Ω的电阻,两种情况下电阻消耗的功率均为80W.求:
如图为一理想变压器,ab为原线圈,ce为副线圈,d为副线圈引出的一个接头.变压器的原线圈两端所加的正弦式交变电压的最大值Um=400V.若只在ce间接一只Rce=400Ω的电阻,或只在de间接一只Rde=225Ω的电阻,两种情况下电阻消耗的功率均为80W.求: