Question

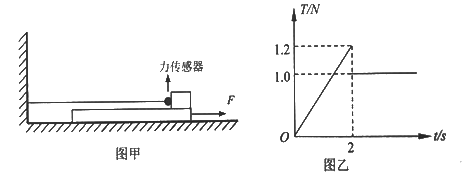
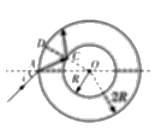
【题目】某种透明材料制成的空心球体内径为 R，外径是内径的 2 倍，其截面（纸面内）如图所示。一束单色光（纸面内）从外球面上 A 点入射，人射角为 45°时，光束经折射后恰好与内球面 B 点相切。

（1）求该透明材料的折射率；

（2）如果在内表面涂上能完全吸光的物质，当一束平行光射向此球时被内表面吸收掉的光束在射进空心球前的横截面积是多少？

（3）在第（1）问的条件下，欲使如图所示的光束能射入空心球内部空心区域，从 A 入射的光线的入射角应满足什么条件？

Answer 1

【答案】（1）。（2） （3）

【解析】

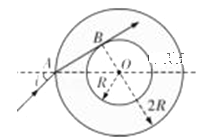
（1）如图所示，设光束经折射后到达内球面上 B 点。在 A 点，由题意知，

入射角 i＝45°，折射角 r＝∠BAO

由几何关系有：=0.5

由折射定律有：

代入数据解得 n＝

（2）

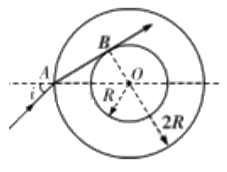
如图所示，平行光束为半径为 R 的空心部分被吸收，不被吸收的极限光线是与 a

球相切的光线 AB，由几何关系有：

Ro=2Rsini

R=2Rsinr

由折射定律有： sini=nsinr

故被吸收掉的光束的橫截面积为：S=2πR2

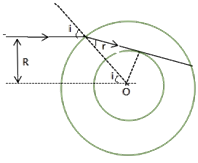
（3）如图所示。设在 A 点的入射角为 i′时，光束经折射后到达内球面上 C 点，并在 C 点恰好发生全反射，则光束在内球面上的入射角∠ACD恰好等于临界角 C。

由 sinC＝得 C＝45°

由正弦定理得……

又 AO＝2CO

由折射定律有……

解得…

因此入射角满足的光线将射入空心球内部。