Question

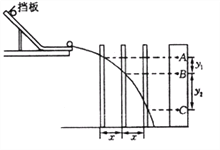
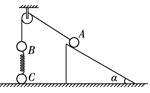
【题目】利用气垫导轨验证机械能守恒定律，实验装置如图甲所示，水平桌面上固定一倾斜的气垫导轨，导轨上A点处有一带长方形遮光条的滑块，其总质量为M，左端由跨过轻质光滑定滑轮的细绳与一质量为

m的小球相连；遮光条两条长边与导轨垂直；导轨上B点有一光电门，可以测量遮光条经过光电门时的挡光时间t，用d表示A点到光电门B处的距离，b表示遮光条的宽度，将遮光条通过光电门的平均速度视为滑块滑过B点时的瞬时速度．实验时滑块在A处由静止开始运动．

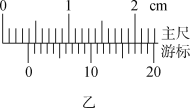
（1）用游标卡尺测量遮光条的宽度b，结果如图乙所示，由此读出b＝________mm．

（2）滑块通过B点的瞬时速度可表示为________．

（3）某次实验测得倾角θ＝30°，重力加速度用g表示，滑块从A处到达B处时，m和M组成的系统动能增加量可表示为ΔEk＝________，系统的重力势能减少量可表示为ΔEp＝________，在误差允许的范围内，若ΔEk＝ΔEp则可认为系统的机械能守恒．

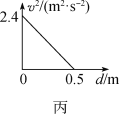
（4）在步骤（3）实验中，某同学改变A、B间的距离，作出的v2—d图象如图丙所示，并测得M＝m，则重力加速度g＝________m/s2．

Answer 1

【答案】（1）3．85 （2） （3） gd （4）9．6

【解析】（1）b＝3 mm＋0．05 mm×17＝3．85 mm

（2）滑块通过B点的瞬时速度v＝

（3）ΔEk＝（m＋M）v2＝

ΔEp＝mgd－Mgdsin 30°＝gd

（4）由ΔEk＝ΔEp得（m＋M）v2＝gd

代入m＝M可得v2＝d

对应v2—d图象可得g＝ m/s2

解得g＝9．6 m/s2