题目内容
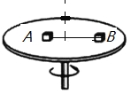
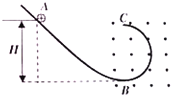
【题目】如图，光滑半圆形轨道与光滑曲面轨道在B处平滑连接，前者置于水平向外的匀强磁场中，有一带正电小球从A静止释放，且能沿轨道前进，并恰能通过半圆轨道最高点C．现若撤去磁场，使球从静止释放仍能恰好通过半圆形轨道最高点，则释放高度H′与原释放高度H的关系是（ ）
A．H′=H B．H′＜H C．H′＞H D．无法确定
【答案】C
【解析】
试题有磁场时，恰好通过最高点，靠重力和洛伦兹力的合力提供向心力，无磁场时，恰好通过重力提供向心力，根据牛顿第二定律求出最高点的临界速度，通过动能定理比较释放点的高度．
解：有磁场时，恰好通过最高点，有：mg﹣qvB=m
，
无磁场时，恰好通过最高点，有：mg=m
，
由两式可知，v2＞v1．
根据动能定理，由于洛伦兹力和支持力不做功，都是只有重力做功，mg（h﹣2R）=
mv2可知，H′＞H．故C正确，A、B、D错误．
故选：C．
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
【题目】在做“研究匀变速直线运动”的实验中：
（1）实验室提供了以下器材：电磁打点计时器、一端附有滑轮的长木板、小车、纸带、细绳、钩码、刻度尺、导线和开关、低压交流电源、复写纸、弹簧测力计。其中在本实验中不需要的器材是________。
（2）如图所示，是某同学由打点计时器得到的表示小车运动过程的一条清晰纸带，纸带上两相邻计数点间还有四个点没有画出，打点计时器打点的时间间隔T＝0.02s，其中x1＝7.05cm、x2＝7.68cm、x3＝8.33cm、x4＝8.95cm、x5＝9.61cm、x6＝10.23cm。
下表列出了打点计时器打下B、C、F时小车的瞬时速度，请在表中填入打点计时器打下D、E两点时小车的瞬时速度（小数点后保留三位数字）。
位置 | B | C | D | E | F |
速度（m·s－1） | 0.737 | 0.801 | 0.992 |
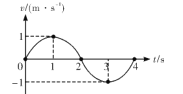
（3）以A点为计时起点，在坐标图中画出小车的速度—时间关系图线。
（4）根据你画出的小车的速度—时间的关系图线计算出的小车的加速度a＝________m/s2。
