题目内容
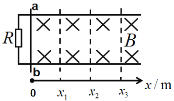
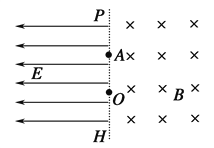
【题目】如图所示,竖直平面xOy内有两个宽度均为![]() 首尾相接的电场区域ABED、BCFE。在ABED场区存在沿轴负y方向、大小为E的匀强电场,在BCFE场区存在大小为
首尾相接的电场区域ABED、BCFE。在ABED场区存在沿轴负y方向、大小为E的匀强电场,在BCFE场区存在大小为![]() E、沿某一方向的匀强电场,且两个电场区域竖直方向均无限大。现有一个质量为m,电荷量为q带正电的粒子以某一初速度从坐标为(0,
E、沿某一方向的匀强电场,且两个电场区域竖直方向均无限大。现有一个质量为m,电荷量为q带正电的粒子以某一初速度从坐标为(0,![]() )的P点射入ABED场区,初速度方向水平向右。粒子恰从坐标为(
)的P点射入ABED场区,初速度方向水平向右。粒子恰从坐标为(![]() ,
,![]() /2)的Q点射入BCFE场区,且恰好做加速直线运动,带电粒子的重力忽略不计,求:
/2)的Q点射入BCFE场区,且恰好做加速直线运动,带电粒子的重力忽略不计,求:

(1)粒子进入ABED区域时的初速度大小;
(2)粒子从CF边界射出时的速度大小。
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1) 在ABED由匀变速曲线运动规律
在水平方向有:L=v0t
在竖直方向有:![]()
由牛顿定律:Eq=ma
联立方程解得:![]() ;
;
(2) 在BCFE区域.对粒子做加速直线运动,设Q点处的速度为v.
由 ![]() 得:
得:![]()
![]() ,方向与水平方向夹角45°斜向下
,方向与水平方向夹角45°斜向下
有几何关系,可知射出点的坐标为![]() ,则在BCFE区域发生的位移为
,则在BCFE区域发生的位移为![]() L.
L.
对粒子由动能定理:
![]()
解得:![]() 。
。

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目