题目内容
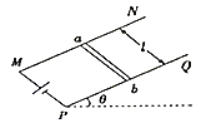
【题目】如图所示，圆形区域半径为
，区域内有一垂直纸面的匀强磁场，磁感应强度的大小为
，
为磁场边界上的最低点。大量质量均为
，电荷量绝对值均为
的带负电粒子，以相同的速率从点射入磁场区域，速度方向沿位于纸面内的各个方向。粒子的轨道半径r=2R，AC为圆形区域水平直径的两个端点，粒子重力不计，空气阻力不计，则
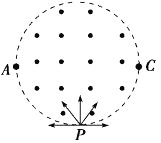
A. 不可能有粒子从
点射出磁场
B. 粒子在磁场中运动的最长时间为
C. 粒子射入磁场的速率为
D. 若粒子的速率可以变化，则可能有粒子从
点水平射出
【答案】BCD
【解析】
由洛仑兹力提供向心力
，当
时，可以求出粒子的速度．至于粒子在圆形磁场区域内的运动时间，由于带电粒子的轨道半径
为一定值且大于磁场区域的半径R，所以当带电粒子的轨迹最长时，时间最长，即以磁场圆直径为弦长的轨迹时间最长，如图所示的以
为圆心的轨迹．
A.若入射速度恰当，则粒子能够通过C点，甚至能够找到圆心：作PC的中垂线，以P或C为圆心以2R为半径画弧交PC中垂线于OC，即通过C点轨迹的圆心，A错误；
BC.由洛仑兹力提供向心力，当时，速度
，要使带电粒子在圆形磁场中的时间最长，则是以磁场圆直径为弦的轨迹时间最长。由几何关系知：此轨迹在磁场的偏转角为60°，所以最长时间
，BC正确；
D.若粒子的速度变为
，则其运动半径为R，若粒子从P点向上入射，则从A点水平穿出，D正确．
练习册系列答案
相关题目
