��Ŀ����
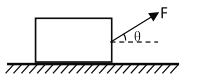
����Ŀ����ͼ��ʾ�����Ϊ��=37�����㹻����б����̶���ˮƽ�����ϣ�Сľ������б�����ϵĺ㶨����F�����£���б���ϵ�A���ɾ�ֹ��ʼ�������ȼ����˶���ǰ����4.0m�ִ�B��ʱ���ٶ�Ϊ8m/s����֪ľ����б���Ķ�Ħ��������=0.5��ľ������m=1kg����g=10m/s2 �� ȡsin37���0.6��cos37���0.8����

��1��ľ�����ܵ�����F���
��2������ľ�鵽��B��ʱ��ȥ����F����ľ�黹����б���ϻ��ľ���S�ͷ���B����ٶȣ�
���𰸡���1��18J ��2��3.2m��![]() m/s
m/s
��������
��1�������ȱ���ֱ���˶����ٶ�λ�ƹ�ʽ����ϻ����ȼ����˶��ļ��ٶȣ����ţ�ٵڶ������������F�Ĵ�С��
��2������ţ�ٵڶ����������ȥ�������ϻ��ļ��ٶȣ�����ٶ�λ�ƹ�ʽ���ľ����б���ϻ��ľ��룬����ţ�ٵڶ���������»�ʱ�ļ��ٶȣ�����ٶ�λ�ƹ�ʽ�������B����ٶȣ�
��1�������ٶ�λ�ƹ�ʽ�ã�ľ���ϻ��ļ��ٶ�![]() ��
��
����ţ�ٵڶ����ɵã�F��mgsin37������mgcos37��=ma1��
���F=mgsin37��+��mgcos37��+ma1=10��0.6+0.5��10��0.8+1��8N=18N��
��2������ȼ����ϻ��ļ��ٶȴ�С
![]() =gsin37��+��gcos37��=10��0.6+0.5��10��8=10m/s2��
=gsin37��+��gcos37��=10��0.6+0.5��10��8=10m/s2��
���Ի�����б���ϻ��ľ���s=![]() ��
��
����������ȼ����˶��ļ��ٶ�![]() =gsin37������gcos37��=10��0.6��0.5��10��0.8=2m/s2��
=gsin37������gcos37��=10��0.6��0.5��10��0.8=2m/s2��
��B����ٶ�![]() =
=![]() m/s
m/s
�𣺣�1��ľ�����ܵ�����FΪ18N��
��2��ľ�黹����б���ϻ��ľ���Ϊ3.2m������B����ٶ�Ϊ![]() m/s��
m/s��

 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�