题目内容
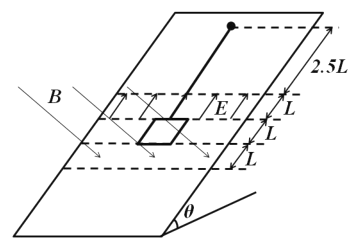
【题目】如图所示,倾角为![]() =30°的足够长的光滑绝缘斜面上存在宽度均为L=0.2m的匀强电场和匀强磁场区域,电场方向平行斜面向上,磁场方向垂直斜面向下,磁感应强度大小B=0.5T。电场的下边界与磁场的上边界相距也为L。电荷量q=2.5×10-4C的带正电小球(视为质点)通过长度为3.5L的绝缘轻杆与边长为L、电阻R=0.02
=30°的足够长的光滑绝缘斜面上存在宽度均为L=0.2m的匀强电场和匀强磁场区域,电场方向平行斜面向上,磁场方向垂直斜面向下,磁感应强度大小B=0.5T。电场的下边界与磁场的上边界相距也为L。电荷量q=2.5×10-4C的带正电小球(视为质点)通过长度为3.5L的绝缘轻杆与边长为L、电阻R=0.02![]() 的正方形线框相连,形成质量m=0.10kg的“
的正方形线框相连,形成质量m=0.10kg的“![]() ”型装置,开始时,线框下边与磁场的上边界重合,现将该装置由静止释放,当线框下边刚离开磁场时恰好做匀速运动;当小球刚要运动到电场的下边界时恰好返回。装置在运动过程中空气阻力不计,求:
”型装置,开始时,线框下边与磁场的上边界重合,现将该装置由静止释放,当线框下边刚离开磁场时恰好做匀速运动;当小球刚要运动到电场的下边界时恰好返回。装置在运动过程中空气阻力不计,求:
(1)线框下边刚离开磁场时做匀速运动的速度大小;
(2)线框从静止释放到线框上边离开磁场所需要的时间;
(3)匀强电场的电场强度大小;
(4)从静止释放经足够长时间后,线框内产生的总热量。
【答案】(1)1m/s;(2)0.6s;(3)4×103N/C;(4)0.2J
【解析】
(1)设线框下边刚离开磁场时做匀速运动的速度大小为v0,根据平衡条件可得
Mgsinθ=BIL
其中
![]()
解得
v0=1m/s
(2)根据动量定理可得
mgsinθt-BILt=mv0
其中
![]()
联立解得
t=0.6s
(3)从线框刚离开磁场到小球刚运动到电场的下边界的过程中,根据动能定理可得:
![]()
解得电场强度
E=4×103N/C
(4)设经过足够长的时间线框最终不会进入磁场,即运动到最高点时线框的上边与磁场的下边重合,小球做上下的往复运动;
mgsinθ2L=Q
解得
Q=0.2J

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目