题目内容
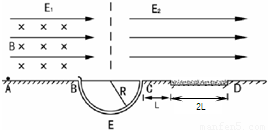
如图,粗糙的水平面AB上的空间中存在场强分别为E1的匀强电场及匀强磁场B,一带正电小球质量为m,所带电荷量为q,刚开始静止在A点,在电场力的作用下开始向右运动,到达B点时进入一埋入地下的半径为R的半圆形软管,且在转角B处无机械能损失,若小球到达B点时恰好对水平面的作用力为 mg,试求:
mg,试求:(1)小球到达B点时的速度大小是多少?
(2)若A、B间距离为S,则小球从A运动到B克服摩擦力做多少功?
(3)在软管的最低点E,软管对小球的作用力是多大?
(4)在CD平面上距离C点L处有一长为2L的沙坑,要使小球落在CD平面上的沙坑外,试求CD上空的匀强电场E2的取值范围.
【答案】分析:(1)根据题意可知,洛伦兹力、支持力与重力处于平衡,因此由洛伦兹力公式可求出速度大小;
(2)小球从A到B过程,由动能定理可求出小球从A运动到B克服摩擦力做的功;
(3)由小球机械能守恒定律与牛顿第二定律及向心力表达式,可求出软管对小球的作用力;
(4)小球从C点冲出后,将运动沿水平方向和竖直方向进行分解,根据分运动的时间相等,由运动学规律可求出匀强电场E2的取值范围.
解答:解(1)由于小球到B点时受洛伦兹力、支持力和重力处于平衡,所以
qVBB+N=mg
又因为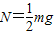
解之得:VB=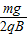
(2)小球从A到B运动过程中,只有摩擦力、电场力做功,由动能定理可得
E1qS-Wf=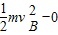
∴Wf=E1qS-
(3)由机械能守恒定律并取E点为零势能点,设软管对小球的作用力为F,可得
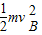 +mgR=
+mgR=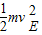 +0
+0
由牛顿第二定律:F-mg=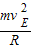
解得:F=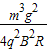 +3mg
+3mg
(4)小球从C点冲出后,在竖直方向上作初速度大小为Vy=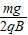 的竖直上抛运动,水平方向上做匀加速直线运动,
的竖直上抛运动,水平方向上做匀加速直线运动,
所以,设在空中飞行的时间为t,
则由t=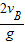 可得
可得
t=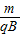
水平方向上,a=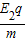 ,
,
小球落到沙坑以外,则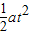 <L或
<L或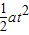 >3L
>3L
可得E2的取值范围为:E2<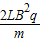 或 E2>
或 E2>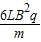
答:(1)小球到达B点时的速度大小是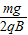 ;
;
(2)若A、B间距离为S,则小球从A运动到B克服摩擦力做功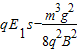 ;
;
(3)在软管的最低点E,软管对小球的作用力是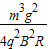 +3mg;
+3mg;
(4)在CD平面上距离C点L处有一长为2L的沙坑,要使小球落在CD平面上的沙坑外,试求CD上空的匀强电场E2的取值范围为:E2<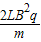 或 E2>
或 E2>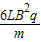 .
.
点评:考查了动能定理、机械能守恒定律、牛顿第二定律、运动学规律,同时涉及到洛伦兹力与速度的关系,将曲线运动的分解两方向的直线运动,本题属于力电综合题,难题,学生容易失分.
(2)小球从A到B过程,由动能定理可求出小球从A运动到B克服摩擦力做的功;
(3)由小球机械能守恒定律与牛顿第二定律及向心力表达式,可求出软管对小球的作用力;
(4)小球从C点冲出后,将运动沿水平方向和竖直方向进行分解,根据分运动的时间相等,由运动学规律可求出匀强电场E2的取值范围.
解答:解(1)由于小球到B点时受洛伦兹力、支持力和重力处于平衡,所以
qVBB+N=mg
又因为
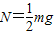
解之得:VB=
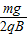
(2)小球从A到B运动过程中,只有摩擦力、电场力做功,由动能定理可得
E1qS-Wf=
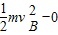
∴Wf=E1qS-

(3)由机械能守恒定律并取E点为零势能点,设软管对小球的作用力为F,可得
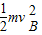 +mgR=
+mgR=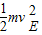 +0
+0 由牛顿第二定律:F-mg=
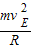
解得:F=
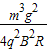 +3mg
+3mg (4)小球从C点冲出后,在竖直方向上作初速度大小为Vy=
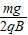 的竖直上抛运动,水平方向上做匀加速直线运动,
的竖直上抛运动,水平方向上做匀加速直线运动,所以,设在空中飞行的时间为t,
则由t=
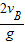 可得
可得t=
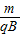
水平方向上,a=
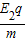 ,
,小球落到沙坑以外,则
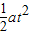 <L或
<L或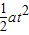 >3L
>3L 可得E2的取值范围为:E2<
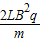 或 E2>
或 E2>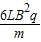
答:(1)小球到达B点时的速度大小是
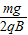 ;
;(2)若A、B间距离为S,则小球从A运动到B克服摩擦力做功
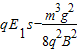 ;
;(3)在软管的最低点E,软管对小球的作用力是
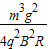 +3mg;
+3mg;(4)在CD平面上距离C点L处有一长为2L的沙坑,要使小球落在CD平面上的沙坑外,试求CD上空的匀强电场E2的取值范围为:E2<
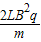 或 E2>
或 E2>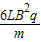 .
.点评:考查了动能定理、机械能守恒定律、牛顿第二定律、运动学规律,同时涉及到洛伦兹力与速度的关系,将曲线运动的分解两方向的直线运动,本题属于力电综合题,难题,学生容易失分.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 如图所示,质量为M的小车静止于光滑的水平面上,小车上AB部分是半径R的四分之一光滑圆弧,BC部分是粗糙的水平面.今把质量为m的小物体从A点由静止释放,m与BC部分间的动摩擦因数为μ,最终小物体与小车相对静止于B、C之间的D点,则B、D间距离x随各量变化的情况是( )
如图所示,质量为M的小车静止于光滑的水平面上,小车上AB部分是半径R的四分之一光滑圆弧,BC部分是粗糙的水平面.今把质量为m的小物体从A点由静止释放,m与BC部分间的动摩擦因数为μ,最终小物体与小车相对静止于B、C之间的D点,则B、D间距离x随各量变化的情况是( ) 如图所示,某物体受到与水平方向成θ角(θ<90°)推力F的作用,沿粗糙的水平面作加速度为a的匀加速直线运动,现在保持F的方向不变,而使F增大到原来的2倍,此后( )
如图所示,某物体受到与水平方向成θ角(θ<90°)推力F的作用,沿粗糙的水平面作加速度为a的匀加速直线运动,现在保持F的方向不变,而使F增大到原来的2倍,此后( ) 如图,粗糙的水平面AB上的空间中存在场强分别为E1的匀强电场及匀强磁场B,一带正电小球质量为m,所带电荷量为q,刚开始静止在A点,在电场力的作用下开始向右运动,到达B点时进入一埋入地下的半径为R的半圆形软管,且在转角B处无机械能损失,若小球到达B点时恰好对水平面的作用力为
如图,粗糙的水平面AB上的空间中存在场强分别为E1的匀强电场及匀强磁场B,一带正电小球质量为m,所带电荷量为q,刚开始静止在A点,在电场力的作用下开始向右运动,到达B点时进入一埋入地下的半径为R的半圆形软管,且在转角B处无机械能损失,若小球到达B点时恰好对水平面的作用力为