题目内容
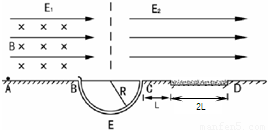
(18分) 如图,粗糙的水平面AB上的空间中存在场强分别为E1的匀强电场及匀强磁场B,一带正电小球质量为m,所带电荷量为q,刚开始静止在A点,在电场力的作用下开始向右运动,到达B点时进入一埋入地下的半径为R的半圆形软管,且在转角B处无机械能损失,若小球到达B点时恰好对水平面的作用力为![]() ,试求:
,试求:
小球到达B点时的速度大小是多少?
若A、B间距离为S,则小球从A运动到B克服摩擦力做多少功?
在软管的最低点E,软管对小球的作用力是多大?
在CD平面上距离C点L处有一长为2L的沙坑,要使小球落在CD平面上的沙坑外,试求CD上空的匀强电场E2的取值范围。

(18分)解(1)由于小球到B点时受洛伦兹力、支持力和重力,所以
qVBB+N=mg ![]() …………2分
…………2分
VB=![]() …………1分
…………1分
(2)小球从A到B运动过程中,只有摩擦力、电场力做功,由动能定理可得
E1qS-Wf=![]() ……………………2分
……………………2分
∴Wf = E1qS-![]() ……………………1分
……………………1分
(3)由机械能守恒定律并取E点为零势能点,设软管对小球的作用力为F,可得
![]() +mgR=
+mgR=![]() +0 ………………2分
+0 ………………2分
F-mg=![]() ………………2分
………………2分
F=![]() +3mg ………………1分
+3mg ………………1分
(4)小球从C点冲出后,在竖直方向上作初速度大小为Vy=![]() 的竖直上抛运动,水平方向上做匀加速直线运动,所以,设在空中飞行的时间为t ,则由t=
的竖直上抛运动,水平方向上做匀加速直线运动,所以,设在空中飞行的时间为t ,则由t=![]() 可得
可得
t=![]() ………………………………2分
………………………………2分
水平方向上,a=![]() , ………………………………2分
, ………………………………2分
小球落到沙坑以外,则![]() <L或
<L或![]() >3L ………………………………2分
>3L ………………………………2分
可得E2的取值范围为: E2<![]() 或 E2>
或 E2>![]() ……………1分
……………1分

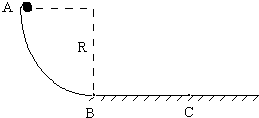 如图所示,质量为m的小球,自A点由静止开始沿半径为R的
如图所示,质量为m的小球,自A点由静止开始沿半径为R的 如图,粗糙的水平面AB上的空间中存在场强分别为E1的匀强电场及匀强磁场B,一带正电小球质量为m,所带电荷量为q,刚开始静止在A点,在电场力的作用下开始向右运动,到达B点时进入一埋入地下的半径为R的半圆形软管,且在转角B处无机械能损失,若小球到达B点时恰好对水平面的作用力为
如图,粗糙的水平面AB上的空间中存在场强分别为E1的匀强电场及匀强磁场B,一带正电小球质量为m,所带电荷量为q,刚开始静止在A点,在电场力的作用下开始向右运动,到达B点时进入一埋入地下的半径为R的半圆形软管,且在转角B处无机械能损失,若小球到达B点时恰好对水平面的作用力为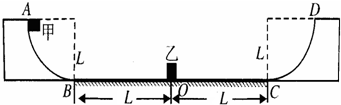
 mg,试求:
mg,试求: