题目内容
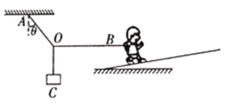
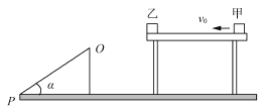
【题目】如图所示,水平面上固定一倾角为![]() =37°的斜面体,在其右侧有一水平的桌面,桌面的左边缘距离斜面体右侧的水平间距设为s(s未知),现将一可视为质点的物块甲由水平桌面右端以初速度v0=6m/s向左滑动,滑到左端时与可视为质点的物块乙发生弹性碰撞,物块乙离开桌面后,经过一段时间,无碰撞地由光滑固定的斜面体顶端O点滑上斜面体,已知桌面两端之间的距离为x=4.0m,
=37°的斜面体,在其右侧有一水平的桌面,桌面的左边缘距离斜面体右侧的水平间距设为s(s未知),现将一可视为质点的物块甲由水平桌面右端以初速度v0=6m/s向左滑动,滑到左端时与可视为质点的物块乙发生弹性碰撞,物块乙离开桌面后,经过一段时间,无碰撞地由光滑固定的斜面体顶端O点滑上斜面体,已知桌面两端之间的距离为x=4.0m,![]() kg,物块甲与水平桌面之间的动摩擦因数为
kg,物块甲与水平桌面之间的动摩擦因数为![]() =0.25。桌面与O点的高度差为h=0.45m,重力加速度为g=10m/s2,sin37°=0.6,cos37°=0.8,忽略空气的阻力。求:
=0.25。桌面与O点的高度差为h=0.45m,重力加速度为g=10m/s2,sin37°=0.6,cos37°=0.8,忽略空气的阻力。求:
(1)物块乙离开桌面时的速度大小和桌面的左边缘距离斜面体右侧的水平间距;
(2)物块甲的质量;
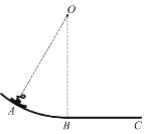
(3)如果O点距离水平面的高度为H=4.8m,求物块甲开始运动到物块乙到达P点的总时间。
【答案】(1)4m/s,1.2m;(2)1kg;(3)2.1s
【解析】
(1)根据题意有
![]()
竖直方向速度
![]()
又
![]()
桌面的左边缘距离斜面体右侧的水平间距为
![]()
(2)设滑块甲在桌面上滑动时的加速度为a,滑块到达桌面的左边缘的速度为![]() 。
。
由牛顿第二定律可知
![]()
又由运动学公式
![]()
由以上整理可得
![]()
由动量守恒与机械能守恒可得
![]()
![]()
解得甲的质量为
![]() kg
kg
(3)物块甲在水平桌面上运动的时间为
![]()
乙到达斜面时的合速度为
![]()
乙在斜面上运动时的加速度为
![]()
斜面的长度为
![]()
由
![]()
解得
![]() (
(![]() 舍去)
舍去)
滑块乙离开平台到达斜面底端的时间为
![]()

练习册系列答案
相关题目