��Ŀ����
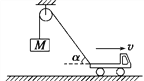
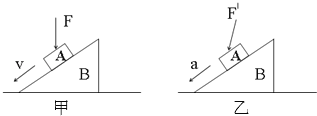
����Ŀ����ͼ��ʾ������M=2.0kg�ij�ľ�徲ֹ�ڹ⻬ˮƽ���ϣ��ڳ�ľ����Ҷ˷�һ����m=1.0kg��С���飨����Ϊ�ʵ㣩��С�����볤ľ��֮��Ķ�Ħ��������=0.20.����ˮƽ����F=8.0N��������ľ�壬ʹС�����볤ľ�巢����Ի���������t=1.0s��ȥ����F.С�������˶�������ʼ��û�дӳ�ľ���ϵ���.��

��1����ȥ��FʱС����ͳ�ľ����ٶȸ�Ϊ����
��2���˶���С����ľ���Ҷ˵��������Ƕ��
���𰸡���1��![]() ��
�� ![]() ��2��
��2��![]()
�������� (1)�Գ�ľ��ʩ�Ӻ���F��ʱ���ڣ�С�����볤ľ�����Ի�����С����ͳ�ľ����ˮƽ��������������ͼ��ʾ��
![]()
С��������Ħ����f=��mg
��С����ļ��ٶ�Ϊa1������ţ�ٵڶ����ɣ�f=ma1
��ã�a1=2.0m/s2
��ľ���ܵ�Ħ����f��=f=��mg
�賤ľ��ļ��ٶ�Ϊa2������ţ�ٵڶ����ɣ�Ff��=Ma2
��ã�a2=3.0m/s2
����ʱ��t=1.0s��
С������ٶ�v1=a1t=2.0m/s
��ľ����ٶ�v2=a2t=3.0m/s
(2)��ȥ��F���һ��ʱ���ڣ�С������ٶ�С�ڳ�ľ����ٶȣ�С�������Լ��ٶ�a1���ȼ���ֱ���˶�����ľ�����ȼ���ֱ���˶����賤ľ���˶��ļ��ٶ�Ϊa3����ʱ��ľ��ˮƽ�������������ͼ��ʾ������ţ�ٵڶ�����
![]()
f��=Ma3
���a3=1.0m/s2
���پ���ʱ��t1��С�����볤ľ����ٶ���ȣ���ʱС������Գ�ľ�徲ֹ
��v1+a1t1=v2a3t1
��ã�t1=1/3s
��ʱ���ߵ��ٶȶ���![]() =8/3m/s��
=8/3m/s��
�����ľ���λ�Ʒֱ�Ϊ��
![]()
![]()
�� ![]()

 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д�