��Ŀ����
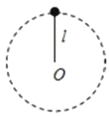
����Ŀ����ͼ��ʾ���ڹ⻬ˮƽ��������һ�̶��ĵ��壬�����Ϲ̶�һ���ᵯ�ɣ�����һ����M=3kg����L=4m��С��AB������OΪС�����е㣬AO���ֲִڣ�OB���ֹ⻬����һ����Ϊm=1kg��С��飨����Ϊ�ʵ㣩�����ڳ�������ˣ�����С���һ����v0=4m/s���ٶ���ˮƽ�������������˶�����ײ�������˲���ٶȱ�Ϊ�㣬��δ�뵲��ճ������֪��OB���ֵij��ȴ��ڵ��ɵ���Ȼ���ȣ�����ʼ�մ��ڵ������ڣ�С����복AO����֮��Ķ�Ħ������Ϊ��=0.3���������ٶ�g=10m/s2 �� ��
��1��С���͵�������õĹ����У����ɾ��е���������ܣ�
��2��С���͵�������õĹ����У����ɶ�С���ij�����
��3��С�������ͣ��С���ϵ�λ�þ�A�˶�Զ��
���𰸡�
��1���⣺��С��飬��ma=����mg
�����˶�ѧ��ʽ ![]()
��������ϵ ![]() ��
��
���EP=2J��
��С���͵�������õĹ����У����ɾ��е����������Ϊ2J
��2���⣺��С����뿪����ʱ���ٶ�Ϊv1���� ![]() ��
��
��С��飬���ݶ������� I=��mv1��mv
�ɢݢ�ʽ���������ݵ�I=��4kgm/s��
���ɶ�С���ij�����СΪ4kgm/s������ˮƽ����
��С���͵�������õĹ����У����ɶ�С���ij�����СΪ4kgm/s������ˮƽ����
��3���⣺С��黬��O���С������ã��ɶ����غ�mv1=��m+M��v2��
��������ϵ ![]()
С�������ͣ��С���Ͼ�A�ľ��� ![]()
���xA=1.5m��
��С�������ͣ��С���ϵ�λ�þ�A��Ϊ1.5m
����������1������ţ�ٵڶ��������С�����AO�����ȼ���ֱ���˶��ļ��ٶȴ�С���Ӷ������˶�ѧ��ʽ���С�����B���ɽӴ�ǰ���ٶȣ����������غ㶨��������ɵ���������ܣ���2��С���͵�������õĹ����У����������غ㶨�����С����뿪����ʱ���ٶȣ����ݶ�������������ɶ�С���ij�������3�����ݶ����غ㶨�����С����С��������Ծ�ֹʱ���ٶȣ����������غ㶨�����С�����С������Ħ�����ֵ����·�̣��Ӷ����С�������λ�þ���A��ľ��룮

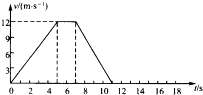
����Ŀ��һ��������ƽֱ�Ĺ�·�ϴӾ�ֹ��ʼ�˶����Ⱥ����ȼ��١����١��ȼ���ֱ���˶������ֹͣ��������������ʼ��ʱ���±���¼������ijЩʱ�̵�˲ʱ�ٶȣ��������ݿ��жϳ������˶���v��tͼ���ǣ� ��
ʱ��/s | 1.0 | 2.0 | 3.0 | 5.0 | 7.0 | 9.5 | 10.5 |
�ٶ�/��MS�� | 3.0 | 6.0 | 9.0 | 12 | 12 | 9.0 | 3.0 |
A.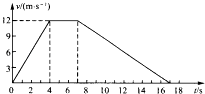
B.
C.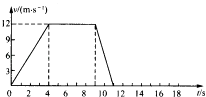
D.