题目内容
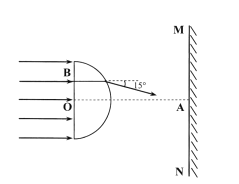
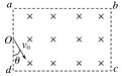
【题目】如图所示,一足够长的矩形区域abcd内充满方向垂直纸面向里、磁感应强度为B的匀强磁场,在ad边中点O沿垂直磁场方向射入一速度跟ad边夹角为θ=30°、大小为v0的带正电粒子,已知粒子质量为m,电量为q,ad边长为L,ab边足够长,粒子重力不计,则( )
A. 若粒子能从ab边上射出磁场,则v0的最小速度应大于![]()
B. 若粒子能从ab边上射出磁场,则v0的最大速度应等于![]()
C. 如果带电离子v0大小不受限制,则粒子在磁场中运动的最长时间为![]()
D. 如果带电粒子v0大小不受限制,则粒子在磁场中运动的最长时间为![]()
【答案】AC
【解析】
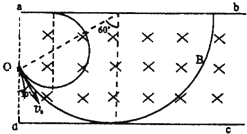
(1)粒子在磁场中做匀速圆周运动,当其轨迹恰好与ab边相切时,轨迹半径最小,对应的速度最小.当其轨迹恰好与cd边相切时,轨迹半径最大,对应的速度最大,由几何知识求出,再牛顿定律求出速度的范围.
(2)粒子轨迹所对圆心最大时,在磁场中运动的最长时间.当其轨迹恰好与ab边相切或轨迹更小时,时间最长,求出圆心角,再求时间.
粒子运动轨迹如图所示:
若粒子速度为v0,则qv0B=m![]() ,所以有
,所以有![]() ;设圆心在O1处对应圆弧与ab边相切,相应速度为v01,则有:R1+R1sinθ=
;设圆心在O1处对应圆弧与ab边相切,相应速度为v01,则有:R1+R1sinθ=![]() ,将
,将![]() 代入上式可得:v01=
代入上式可得:v01=![]() ,同理,设圆心在O2处对应圆弧与cd边相切,相应速度为v02,则有:R2-R2sinθ=
,同理,设圆心在O2处对应圆弧与cd边相切,相应速度为v02,则有:R2-R2sinθ=![]() ,将
,将![]() 代入上式可得:v02=
代入上式可得:v02=![]() ,所以粒子能从ab边上射出磁场的v0应满足:
,所以粒子能从ab边上射出磁场的v0应满足:![]() ≤v≤
≤v≤![]() ,故A正确,B错误;由t=
,故A正确,B错误;由t=![]() T及T=
T及T=![]() 可知,粒子在磁场中经过的弧所对的圆心角α越长,在磁场中运动的时间也越长。在磁场中运动的半径r≤R1时,运动时间最长,弧所对圆心角为:α=(2π-2θ)=
可知,粒子在磁场中经过的弧所对的圆心角α越长,在磁场中运动的时间也越长。在磁场中运动的半径r≤R1时,运动时间最长,弧所对圆心角为:α=(2π-2θ)=![]() ,所以最长时间为:t=
,所以最长时间为:t=![]() T=
T=![]() ,故C正确,D错误;故选AC。
,故C正确,D错误;故选AC。

练习册系列答案
相关题目