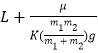��Ŀ����
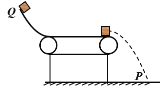
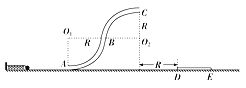
����Ŀ����ͼ��ʾ�������뾶��ΪR���ķ�֮һԲ�����ɵĹ⻬ϸ�ܵ�ABC��ֱ���ã��ҹ̶��ڹ⻬ˮƽ���ϣ�Բ������O1O2ˮƽ���ᵯ����˹̶�����ֱ�����ϣ��Ҷ���һ����Ϊm��С��Ӵ�(��˩�ӣ�С���ֱ����С�ڹܵ��ھ�)����ΪR�ı���DE�̶���ˮƽ���ϣ�������D���ܵ��Ҷ�C��ˮƽ����ΪR���������������ƶ�С��ʹ����ѹ����ijһλ�ã�Ȼ��ſ���С���ɵ��������ܵ�������C���׳����������ٶ�Ϊg
(1)С��C��ʱ���ܵĵ����Ĵ�СΪ![]() mg���ɵ������ܵĴ�СEp��
mg���ɵ������ܵĴ�СEp��
(2)��������ͬ������С��Ȼ���Խ�����ѹ������ͬ��λ���ͷţ�С��C���׳��ܻ��б���DE����С������m1��ȡֵ��Χ��
���𰸡�(1) ![]() mgR (2)
mgR (2) ![]() m��m1��
m��m1��![]() m
m
��������
��1����C�㣬��С��Ϊ�о���������: mg+![]() mg=m
mg=m![]()
���������̣����������غ㶨�ɵ� Ep=2mgR+![]() mvC2
mvC2
������� Ep=![]() mgR
mgR
��2��С���뿪C�����ƽ���˶���
��ֱ����2R��![]() gt2��
gt2��
ˮƽ����x1=v1t��
��ҪС����б��壬Ӧ���㣺R��x1��2R��
��ã�![]()
��A��C�Ĺ����У����������غ㶨�ɵã�
EP��2m1gR+![]() m1v12
m1v12
��ã�![]() m��m1��
m��m1��![]() m
m

����Ŀ���ƺ��ʻ�ᵼ�����లȫ����������Ϊ��ʻԱ�ķ�Ӧʱ��䳤����Ӧʱ����ָ��ʻԱ�ӷ����������ȡ�ƶ���ʱ�䣮�±�����˼����������ָ��ʻԱ�ӷ����������ȡ�ƶ���ʱ����������ʻ�ľ��룬���ƶ���������ָ��ʻԱ�ӷ������������ֹͣ��ʻ�ľ��루���������ƶ�ʱ�ļ��ٶȴ�С����ͬ����
�ٶ�/��ms��1�� | ˼������/m | �ƶ�����/m | ||
���� | �ƺ� | ���� | �ƺ� | |
15 | 7.5 | 15.0 | 22.5 | 30.0 |
20 | 10.0 | 20.0 | 36.7 | 46.7 |
25 | 12.5 | 25.0 | 54.2 | 66.7 |
�����ϱ���֪������˵����ȷ���ǣ�������
A. ��ʻԱ��������·�Ӧʱ��Ϊ0.5 s
B. ��ʻԱ�ƺ�Ӧʱ�����������¶�0.5 s
C. ��ʻԱ��ȡ�ƶ���ʩ�������ļ��ٶȴ�СΪ3.75 m/s2
D. ��������25 m/s���ٶ���ʻʱ������ǰ��60 m�������飬�ƺ��ʻ���ܰ�ȫͣ��