题目内容
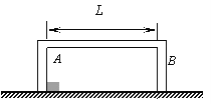
【题目】有尺寸可以忽略的小物块A，放在足够长的水平地面上．取一无盖的长方形木盒B将A罩住．B的左右内壁间的距离为L．B的质量与A相同．A与地面间的滑动摩擦系数μA，B与地面间的滑动摩擦系数为μB，且μB>μA．开始时，A的左端与B的左内壁相接触（如图所示），两者以相同的初速度υ0向右运动．已知A与B的内壁发生的碰撞都是完全弹性的，且碰撞时间都极短．A与B的其它侧面之间均无接触，重力加速度为g．
（1）经过多长时间A、B发生第一次碰撞（设碰撞前A、B均未停下）
（2）A和B右侧第一次相碰后，若A还能够和B的左端相遇，试通过定量讨论说明此次相遇时A、B两个物体的速率哪个大些？还是等大？
（3）要使A、B同时停止，而且A与B间轻轻接触（即无作用力），求初速υ0的所有可能的值。（用含有L、μB、μA和g的代数式表示）
【答案】（1）
（2）等大；（3）
,n为正整数
【解析】
（1）对A：
，
对B：
， 
，
解得：
（2）设A、B第一次在右壁相碰前的速度分别为υ1和υ2，碰后速度分别为υ3和υ4，
得： 
设经过时间t2，A与B的左侧相遇，此时A、B的速度分别为υ5、υ6，则：
代入得t1=t2
所以有：
，
显然v5=v6
（3）每次A与B的左侧相遇时二者的速度都相同，且比前一次相遇时的速度减小
Δv0=（μA+μB）gt1
为满足题中要求，只要某次A与B的左侧相遇时二者的速度都恰好等于0即可，即需要v0=nΔv0，其中n=1、2、3……
代入得：
，n为正整数.
练习册系列答案
相关题目
