题目内容
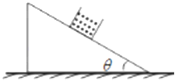
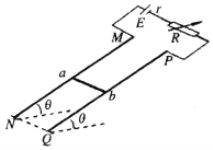
【题目】如图所示,两根光滑直金属导轨MN、PQ平行倾斜放置,它们所构成的轨道平面与水平面之间的夹角θ=37°,两轨道之间的距离L=0.5m。一根质量m=0.02kg的均匀直金属杆ab放在两导轨上,并与导轨垂直,且接触良好,整套装置处于与金属杆垂直的匀强磁场中。在导轨的上端接有电动势E=4V、内阻r=1Ω的直流电源和电阻箱R.已知导轨与金属杆的电阻均可忽略不计,(sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2.)金属杆ab始终静止在导轨上。
(1)如果电阻箱接入电路中的电阻R=3Ω,磁场的方向可以随意调整,求满足条件的磁感应强度的最小值及方向。
(2)如果磁场方向竖直向下,磁感应强度B=0.4T,金属导轨与杆的动摩擦因数μ=0.5,求为使金属杆静止,电阻箱接入电路中的电阻R的范围。(设最大静摩擦力等于滑动摩擦力)
【答案】(1)B=0.24T,方向垂直于导轨平面向下 (2)1Ω~21Ω
【解析】
(1)导体棒静止在斜面上,受到重力、安培力、支持力,当安培力恰好等于重力的分力时,此时磁感应强度B有最小值,即BIL=mgsinθ,
解得:B=0.24T, 方向垂直于导轨平面向下
(2)当摩擦力向上最大,磁场力达到最小,则电流也就达到最小,此时电阻有最大值,根据平衡可知:
mgsinθ=BI1Lcosθ+f1,
f1=μ(mgcosθ+BI1Lsinθ)
![]()
代入数据解得:R1=21Ω,
当摩擦力向下最大,此时安培力有最大值,则电流有最大值,即电阻有最小值根据平衡可知:
mgsinθ=BI2Lcosθ-f2,
f2=μ(mgcosθ+BI2Lsinθ)
![]()
代入数据解得:R2=1Ω,
所以R的范围应该在1Ω到21Ω间
故本题答案是:(1)B=0.24T,方向垂直于导轨平面向下 (2)1Ω~21Ω

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案