题目内容
13.一辆值勤的警车停在公路边,当警员发现从他旁边以15m/s的速度匀速行驶的货车严重超载时,决定前去追赶,经过2s后警车发动起来,并以3m/s2的加速度做匀加速运动,但警车的行驶速度必须控制在108km/h 以内.问:(1)警车在追赶货车的过程中,两车间的最大距离是多少?
(2)警车发动后要多长时间才能追上货车?
分析 (1)在两车速度相等前,货车的速度大于警车,两车的距离越来越大,速度相等之后,货车的速度小于警车,两车的距离越来越小,所以两车速度相等时,距离最大.根据速度相等求出时间,再根据运动学的位移公式求出相距的最大距离.
(2)根据警车追上货车时,两车的位移相等列式即可求解.
解答 解:(1)警车在追赶货车的过程中,当两车速度相等时,它们间的距离最大,设警车发动后经过t1时间两车的速度相等.
则t1=$\frac{15}{3}$ s=5 s
s货=(2+5)×15 m=105 m
s警=$\frac{1}{2}$at12=$\frac{1}{2}$×3×52 m=37.5 m
所以两车间的最大距离△s=s货-s警=105-37.5=67.5 m.
(2)v0=108 km/h=30 m/s,当警车刚达到最大速度时,运动时间t2=$\frac{30}{3}$ s=10 s
s′货=(2+10)×15 m=180 m
s′警=$\frac{1}{2}$at22=$\frac{1}{2}$×3×102 m=150 m
因为s′货>s′警,故此时警车尚未赶上货车,且此时两车距离
△s′=s′货-s′警=30 m
警车达到最大速度后做匀速运动,设再经过△t时间追赶上货车,则
△t=$\frac{△s′}{{v}_{0}-v}$=$\frac{30}{15}$=2 s
所以警车发动后要经过t=t2+△t=10+2=12 s才能追上货车.
答:(1)警车在追赶货车的过程中,两车间的最大距离是67.5m;
(2)警车发动后要12s时间才能追上货车.
点评 解决本题的关键知道速度小者加速追速度大者,两者速度相等时,距离最大.以及知道警车追上货车时,两车的位移相等.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案| A. | 即时速度的大小是$\sqrt{5}$v0 | B. | 运动的时间是$\frac{2{v}_{0}}{g}$ | ||
| C. | 竖直分速度的大小等于2v0 | D. | 运动的位移是$\frac{\sqrt{2}{v}_{0}^{2}}{g}$ |
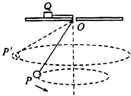 如图所示,一根细线下端拴一个金属小球P,细线的上端固定在金属块Q上,Q放在带小孔(小孔光滑)的固定水平桌面上,小球在某一水平面内做匀速圆周运动(圆锥摆),现使小球改到一个更高一些的水平面上做匀速圆周运动(图中P′位置),两次金属块Q都静止在桌面上的同一点,则后一种情况与原来相比较,下面的判断中正确的是( )
如图所示,一根细线下端拴一个金属小球P,细线的上端固定在金属块Q上,Q放在带小孔(小孔光滑)的固定水平桌面上,小球在某一水平面内做匀速圆周运动(圆锥摆),现使小球改到一个更高一些的水平面上做匀速圆周运动(图中P′位置),两次金属块Q都静止在桌面上的同一点,则后一种情况与原来相比较,下面的判断中正确的是( )| A. | 细线所受的拉力变小 | B. | 小球P运动的角速度变小 | ||
| C. | Q受到桌面的支持力变大 | D. | Q受到桌面的静摩擦力变大 |
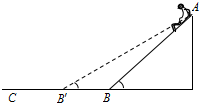 如图,某滑草场有两个坡度不同的滑道AB′和AB(均可看作斜面).质量不同的甲、乙两名游客先后乘坐同一滑草板从A点由静止开始分别沿AB′和AB滑下,最后都停在水平草面BC上,斜草面和水平草面平滑连接,下列说法正确的是( )
如图,某滑草场有两个坡度不同的滑道AB′和AB(均可看作斜面).质量不同的甲、乙两名游客先后乘坐同一滑草板从A点由静止开始分别沿AB′和AB滑下,最后都停在水平草面BC上,斜草面和水平草面平滑连接,下列说法正确的是( )| A. | 沿斜面下滑的时间甲一定比乙长 | |
| B. | 甲、乙两人经过斜面底端时的速率一定相等 | |
| C. | 甲和乙在整个滑行过程中的水平位移大小一定相等 | |
| D. | 沿斜面下滑过程中克服摩擦力做的功甲一定比乙小 |
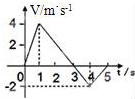
| A. | 0~1 s内的加速度大小是1~3 s内的加速度大小的2倍 | |
| B. | 0~1 s与4~5 s内,质点的加速度方向相反 | |
| C. | 0.5 s与2 s时刻,质点的速度方向相反 | |
| D. | 质点在0~5 s内的平均速度是0.8 m/s: |
| A. | 类似于平抛运动 | B. | 匀速圆周运动 | C. | 匀加速直线运动 | D. | 匀减速直线运动 |
