题目内容
 如图所示,在xoy平面直角坐标系第一象限内分布有垂直向外的匀强磁场,磁感应强度大小B=2.5×10-2T,在第二象限紧贴y轴和x轴放置一对平行金属板MN(中心轴线过y轴),极板间距d=0.4m,极板与左侧电路相连接.通过移动滑动头P可以改变极板MN间的电压.a、b为滑动变阻器的最下端和最上端(滑动变阻器的阻值分布均匀),a、b两端所加电压U=
如图所示,在xoy平面直角坐标系第一象限内分布有垂直向外的匀强磁场,磁感应强度大小B=2.5×10-2T,在第二象限紧贴y轴和x轴放置一对平行金属板MN(中心轴线过y轴),极板间距d=0.4m,极板与左侧电路相连接.通过移动滑动头P可以改变极板MN间的电压.a、b为滑动变阻器的最下端和最上端(滑动变阻器的阻值分布均匀),a、b两端所加电压U=
| ||
| 3 |
| q |
| m |
(1)当滑动头P在ab正中间时,求粒子射入磁场时速度的大小.
(2)当滑动头P在ab间某位置时,粒子射出极板的速度偏转角为α,试写出粒子在磁场中运动的时间与α的函数关系,并由此计算粒子在磁场中运动的最长时间.
分析:(1)当滑动头P在ab正中间时,粒子在电场中做类平抛运动,水平方向做匀速直线运动,位移大小为L,竖直方向做初速度为零的匀加速直线运动,根据牛顿第二定律和运动学结合可求出粒子进入磁场时的速度大小.
(2)当滑动头P在a端时,平行金属板MN板间电压为零,粒子匀速运动,以速度v0进入磁场中,由牛顿第二定律求出轨迹半径.当滑动头P在ab间某一位置时,由牛顿第二定律得到轨迹半径与α的关系式,由几何关系求出粒子在磁场中运动时轨迹圆心角,即可得到粒子在磁场中运动时间的表达式.当板间电压最大时,根据类平抛运动的规律得到粒子射出极板时速度最大的偏转角,即可求出粒子在磁场中运动的最长时间.
(2)当滑动头P在a端时,平行金属板MN板间电压为零,粒子匀速运动,以速度v0进入磁场中,由牛顿第二定律求出轨迹半径.当滑动头P在ab间某一位置时,由牛顿第二定律得到轨迹半径与α的关系式,由几何关系求出粒子在磁场中运动时轨迹圆心角,即可得到粒子在磁场中运动时间的表达式.当板间电压最大时,根据类平抛运动的规律得到粒子射出极板时速度最大的偏转角,即可求出粒子在磁场中运动的最长时间.
解答: 解:(1)当滑动头P在ab正中间时,极板间电压U′=
解:(1)当滑动头P在ab正中间时,极板间电压U′=
U,粒子在电场中做类平抛运动,设粒子射入磁场时沿y轴方向的分速度为vy:
q
=ma ①
vy=at ②
L=v0t ③
粒子射入磁场时速度的大小设为v=
④
联立解得:v=
×104m/s≈2.1×104m/s ⑤
(2)当滑动头P在a端时,粒子在磁场中运动的速度大小为v0,有
qv0B=
⑥
解得:R0=
=0.2m
设粒子射出极板时速度的大小为v,偏向角为α,在磁场中圆周运动半径为R.根据速度平行四边形可得:
v=
⑦
又qvB=
,得R=
⑧
由⑥⑦⑧可得:R=
⑨
粒子在磁场中做圆周运动的轨迹如图所示,圆心为O′,与x轴交点为D,
设∠O′DO=β,根据几何关系:
+
tanα=Rcosα+Rsinβ ⑩
又:
=
=R0
解得:sinα=sinβ,得 β=α
粒子在磁场中运动的周期为T:T=
粒子在磁场中轨迹对应的圆心角为 θ=
+2α
则粒子在磁场中运动的时间:t=
T=
T,得t=
由此结果可知,粒子射入磁场时速度偏转角α越大,则粒子在磁场中运动的时间就越大.假设极板间电压为最大值U=
×102V
时粒子能射出电场,则此粒子在磁场中运动的时间最长.
由(1)问规律可知当滑动头P在b端时,粒子射入磁场时沿y方向的分速度:vym=
×104m/s
y方向偏距:ym=
?
=
m<0.2m,说明粒子可以射出极板.此时粒子速度偏转角最大,设为αm,则
tanam=
=
,得αm=
故粒子在磁场中运动的最长时间:tm=
,得tm=
代入数值得:tm=
×10-4s≈2.6×10-5s.
答:
(1)当滑动头P在ab正中间时,粒子射入磁场时速度的大小是2.1×104m/s.
(2)粒子在磁场中运动的时间与α的函数关系是
,粒子在磁场中运动的最长时间是2.6×10-5s.
 解:(1)当滑动头P在ab正中间时,极板间电压U′=
解:(1)当滑动头P在ab正中间时,极板间电压U′=| 1 |
| 2 |
q
| U′ |
| d |
vy=at ②
L=v0t ③
粒子射入磁场时速度的大小设为v=
|
联立解得:v=
|
(2)当滑动头P在a端时,粒子在磁场中运动的速度大小为v0,有
qv0B=
m
| ||
| R0 |
解得:R0=
| mv0 |
| qB |
设粒子射出极板时速度的大小为v,偏向角为α,在磁场中圆周运动半径为R.根据速度平行四边形可得:
v=
| v0 |
| cosα |
又qvB=
| mv2 |
| R |
| mv |
| qB |
由⑥⑦⑧可得:R=
| R0 |
| cosα |
粒子在磁场中做圆周运动的轨迹如图所示,圆心为O′,与x轴交点为D,
设∠O′DO=β,根据几何关系:
| d |
| 2 |
| L |
| 2 |
又:
| d |
| 2 |
| L |
| 2 |
解得:sinα=sinβ,得 β=α
粒子在磁场中运动的周期为T:T=
| 2πm |
| qB |
粒子在磁场中轨迹对应的圆心角为 θ=
| π |
| 2 |
则粒子在磁场中运动的时间:t=
| θ |
| 2π |
| ||
| 2π |
| m(π+4α) |
| 2qB |
由此结果可知,粒子射入磁场时速度偏转角α越大,则粒子在磁场中运动的时间就越大.假设极板间电压为最大值U=
| ||
| 3 |
时粒子能射出电场,则此粒子在磁场中运动的时间最长.
由(1)问规律可知当滑动头P在b端时,粒子射入磁场时沿y方向的分速度:vym=
2
| ||
| 3 |
y方向偏距:ym=
| vym |
| 2 |
| L |
| v0 |
| ||
| 15 |
tanam=
| vym |
| v0 |
| ||
| 3 |
| π |
| 6 |
故粒子在磁场中运动的最长时间:tm=
| m(π+4αm) |
| 2qB |
| 5πm |
| 6qB |
代入数值得:tm=
| π |
| 12 |
答:
(1)当滑动头P在ab正中间时,粒子射入磁场时速度的大小是2.1×104m/s.
(2)粒子在磁场中运动的时间与α的函数关系是
| m(π+4α) |
| 2qB |
点评:本题的解题关键是准确画出粒子运动的基础上,根据几何知识得到粒子在磁场中运动的时间与α的关系式,难度较大.

练习册系列答案
相关题目
 (2013?安徽模拟)如图所示,在xoy平面上,直线OM与x轴正方向夹角为45°,直线OM左侧存在平行y轴的匀强电场,方向沿y轴负方向.直线OM右侧存在垂直xoy平面向里的磁感应强度为B的匀强磁场.一带电量为q质量为m带正电的粒子(忽略重力)从原点O沿x轴正方向以速度vo射入磁场.此后,粒子穿过磁场与电场的边界三次,恰好从电场中回到原点O.(粒子通过边界时,其运动不受边界的影响)试求:
(2013?安徽模拟)如图所示,在xoy平面上,直线OM与x轴正方向夹角为45°,直线OM左侧存在平行y轴的匀强电场,方向沿y轴负方向.直线OM右侧存在垂直xoy平面向里的磁感应强度为B的匀强磁场.一带电量为q质量为m带正电的粒子(忽略重力)从原点O沿x轴正方向以速度vo射入磁场.此后,粒子穿过磁场与电场的边界三次,恰好从电场中回到原点O.(粒子通过边界时,其运动不受边界的影响)试求: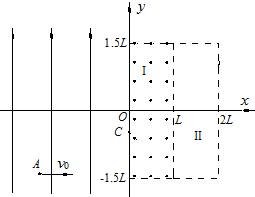 如图所示,在xOy平面的y轴左侧存在沿y轴正方向的匀强电场,y轴右侧区域Ⅰ内存在磁感应强度大小B1=
如图所示,在xOy平面的y轴左侧存在沿y轴正方向的匀强电场,y轴右侧区域Ⅰ内存在磁感应强度大小B1= (2006?连云港二模)如图所示,在xoy平面上,一个以原点O为中心、半径为R的圆形区域内存在着一匀强磁场.磁场的磁感应强度为B,方向垂直于xoy平面向里.在O点处原来静止着一个具有放射性的原子核--氮(
(2006?连云港二模)如图所示,在xoy平面上,一个以原点O为中心、半径为R的圆形区域内存在着一匀强磁场.磁场的磁感应强度为B,方向垂直于xoy平面向里.在O点处原来静止着一个具有放射性的原子核--氮( 如图所示,在xOy平面上,一个以原点O为圆心,半径为4R的原型磁场区域内存在着匀强磁场,磁场的方向垂直于纸面向里,在坐标(-2R,0)的A处静止着一个具有放射性的原子核氮713N.某时刻该核发生衰变,放出一个正电子和一个反冲核,已知正电子从A处射出时速度方向垂直于x轴,且后来通过了y轴,而反冲核刚好不离开磁场区域.不计重力影响和离子间的相互作用.
如图所示,在xOy平面上,一个以原点O为圆心,半径为4R的原型磁场区域内存在着匀强磁场,磁场的方向垂直于纸面向里,在坐标(-2R,0)的A处静止着一个具有放射性的原子核氮713N.某时刻该核发生衰变,放出一个正电子和一个反冲核,已知正电子从A处射出时速度方向垂直于x轴,且后来通过了y轴,而反冲核刚好不离开磁场区域.不计重力影响和离子间的相互作用.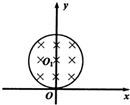 如图所示,在xOy平面上,以y轴上点Ol为圆心,半径为R=0.3m的圆形区域内,分布着一个方向垂直于xOy平面向里,磁感应强度大小为B=0.5T的匀强磁场.一个比荷
如图所示,在xOy平面上,以y轴上点Ol为圆心,半径为R=0.3m的圆形区域内,分布着一个方向垂直于xOy平面向里,磁感应强度大小为B=0.5T的匀强磁场.一个比荷