题目内容
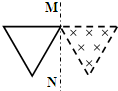
匀强磁场的磁感应强度为B,方向竖直向上,在磁场中有一个总电阻为R、每边长为L的正方形金属框abcd,其中ab、cd边质量均为m,其它两边质量不计,cd边装有固定的水平轴.现将金属框从水平位置无初速释放,如图所示,若不计一切摩擦,金属框经时间t刚好到达竖直面位置a′b′cd.
(1)ab边到达最低位置时感应电流的方向;
(2)求在时间t内流过金属框的电荷量;
(3)若在时间t内金属框产生的焦耳热为Q,求ab边在最低位置时受的磁场力多大?

(1)ab边到达最低位置时感应电流的方向;
(2)求在时间t内流过金属框的电荷量;
(3)若在时间t内金属框产生的焦耳热为Q,求ab边在最低位置时受的磁场力多大?

(1)根据右手定则判断可知:ab边到达最低位置时感应电流的方向由a′到b′.
(2)由q=I△t=
△t,E=
,△φ=BS-0=BL2
整理得:在时间t内流过金属框的电荷量为:q=
(3)由能的转化与守恒定律得:mgL=
mυ2+Q
又由感应电动势为 E=BυL,瞬时电流的大小为 I=
,ab边所受安培力的大小为 F=BIL
整理得:F=
答:
(1)ab边到达最低位置时感应电流的方向由a′到b′;
(2)在时间t内流过金属框的电荷量为
;
(3)若在时间t内金属框产生的焦耳热为Q,ab边在最低位置时受的磁场力为
.
(2)由q=I△t=
| E |
| R |
| △φ |
| △t |
整理得:在时间t内流过金属框的电荷量为:q=
| BL2 |
| R |
(3)由能的转化与守恒定律得:mgL=
| 1 |
| 2 |
又由感应电动势为 E=BυL,瞬时电流的大小为 I=
| E |
| R |
整理得:F=
| B2L2 |
| R |
2gL-
|
答:
(1)ab边到达最低位置时感应电流的方向由a′到b′;
(2)在时间t内流过金属框的电荷量为
| BL2 |
| R |
(3)若在时间t内金属框产生的焦耳热为Q,ab边在最低位置时受的磁场力为
| B2L2 |
| R |
2gL-
|

练习册系列答案
相关题目