题目内容
2. 某同学用如图所示装置验证动量守恒定律,用轻质细线将小球1悬挂于O点,使小球1的球心到悬点O的距离为L,被碰小球2放在光滑的水平桌面上.将小球1从右方的A点(OA与竖直方向的夹角为α)由静止释放,摆到最低点时恰与小球2发生正碰,碰撞后,小球1继续向左运动到C位置(OC与竖直方向夹角为θ),小球2落到水平地面上,落点D到桌面边缘水平距离为s,已知重力加速度为g.
某同学用如图所示装置验证动量守恒定律,用轻质细线将小球1悬挂于O点,使小球1的球心到悬点O的距离为L,被碰小球2放在光滑的水平桌面上.将小球1从右方的A点(OA与竖直方向的夹角为α)由静止释放,摆到最低点时恰与小球2发生正碰,碰撞后,小球1继续向左运动到C位置(OC与竖直方向夹角为θ),小球2落到水平地面上,落点D到桌面边缘水平距离为s,已知重力加速度为g.(1)实验中已经测得上述物理量中的θ、α、L、s以及小球1的质量m1和小球2的质量m2,为了验证两球碰撞过程动量守恒,还应该测量的物理量有小球1质量m1,小球2质量m2,桌面高度h,OC与OB夹角.
(2)请用测得的物理量结合已知物理量分别表示碰撞前后小球1的动量:p1=m1$\sqrt{2gL(1-cosα)}$,p1′=m1$\sqrt{2gL(1-cosθ)}$;再用物理量表示碰
撞前后小球2的动量:p2=0,p2′=m2s•$\sqrt{\frac{g}{2h}}$.
分析 A球下摆过程机械能守恒,根据守恒定律列式求最低点速度;球A上摆过程机械能再次守恒,可求解碰撞后速度;碰撞后小球B做平抛运动,根据平抛运动的分位移公式求解碰撞后B球的速度,然后验证动量是否守恒即可.
解答 解:(1)为了验证两球碰撞过程动量守恒,需要测量两小球的质量,小球1质量m1,小球2质量m2,小球1碰撞前后的速度可以根据机械能守恒定律测出,所以还需要测量OC与OB夹角,需要通过平抛运动测量出小球2碰后的速度,需要测量水平位移S和桌面的高度h.
(2)小球从A处下摆过程只有重力做功,机械能守恒,由机械能守恒定律得:
m1gL(1-cosα)=$\frac{1}{2}$m1v12,解得v1=$\sqrt{2gL(1-cosα)}$.则P1=m1v1=m1$\sqrt{2gL(1-cosα)}$.
小球A与小球B碰撞后继续运动,在A碰后到达最左端过程中,机械能再次守恒,
由机械能守恒定律得:-m1gL(1-cosβ)=0-$\frac{1}{2}$mv1′2,解得v1′=$\sqrt{2gL(1-cosθ)}$,则P1′=m1$\sqrt{2gL(1-cosθ)}$.
碰前小球B静止,则PB=0;
碰撞后B球做平抛运动,水平方向:S=v2′t,竖直方向 h=$\frac{1}{2}$gt2,联立解得v′2=s•$\sqrt{\frac{g}{2h}}$,则碰后B球的动量P2′=m2s•$\sqrt{\frac{g}{2h}}$.
故答案为:
(1)小球1质量m1,小球2质量m2,桌面高度h,OC与OB夹角.
(2)m1$\sqrt{2gL(1-cosα)}$.m1$\sqrt{2gL(1-cosθ)}$.0,m2s•$\sqrt{\frac{g}{2h}}$.
点评 本题解题的关键是要明确两小球的运动过程以及过程中机械能何时守恒,动量何时守恒.

 阅读快车系列答案
阅读快车系列答案| A. | 物体的加速度不断增大 | B. | 物体水平方向做匀速直线运动 | ||
| C. | 物体的竖直方向是自由落体运动 | D. | 物体做匀变速曲线运动 |
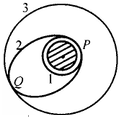 我国发射了一颗地球资源探测卫星,发射时,先将卫星发射至距离地面50km的近地圆轨道1上,然后变轨到近地点距离地面50km、远地点距离地面1500km的椭圆轨道2上,最后由轨道2进入半径为7900km的圆轨道3,轨道1、2相切于P点,轨道2、3相切于Q点.忽略空气阻力和卫星质量的变化,则以下说法正确的是( )
我国发射了一颗地球资源探测卫星,发射时,先将卫星发射至距离地面50km的近地圆轨道1上,然后变轨到近地点距离地面50km、远地点距离地面1500km的椭圆轨道2上,最后由轨道2进入半径为7900km的圆轨道3,轨道1、2相切于P点,轨道2、3相切于Q点.忽略空气阻力和卫星质量的变化,则以下说法正确的是( )| A. | 该卫星从轨道1变轨到轨道2需要在P处点火加速 | |
| B. | 该卫星在轨道2上稳定运行时,P点的速度小于Q点的速度 | |
| C. | 该卫星在轨道2上Q点的加速度大于在轨道3上Q点的加速度 | |
| D. | 该卫星在轨道3的机械能小于在轨道1的机械能 |

| A. | 质点P的振幅为6cm | B. | 横波传播的波速为1m/s | ||
| C. | 横波沿x轴负方向传播 | D. | 在任意4s内P运动的路程为24cm |
 如图所示,一质量M=3.0kg的长方形木板B停放在光滑水平地面上,在其右端放一个质量m=1.0kg的小木块A.现给A以大小为v0=4.0m/s的初速度向左运动,则B的速度可能为( )
如图所示,一质量M=3.0kg的长方形木板B停放在光滑水平地面上,在其右端放一个质量m=1.0kg的小木块A.现给A以大小为v0=4.0m/s的初速度向左运动,则B的速度可能为( )| A. | 0.8 m/s | B. | 1.0 m/s | C. | 2.0 m/s | D. | 4.0 m/s |
 如图是密立根油滴实验的示意图.油滴从喷雾器的喷嘴喷出,落到图中的匀强电场中,调节两板间的电压,通过显微镜观察到某一油滴静止在电场中.下列说法正确的是( )
如图是密立根油滴实验的示意图.油滴从喷雾器的喷嘴喷出,落到图中的匀强电场中,调节两板间的电压,通过显微镜观察到某一油滴静止在电场中.下列说法正确的是( )| A. | 油滴带正电 | |
| B. | 油滴带负电 | |
| C. | 该实验测得油滴所带电荷量等于元电荷的整数倍 | |
| D. | 只要测出两板间的距离和电压就能求出油滴的电量 |

 如图所示为一小球做平抛运动的闪光照相照片的一部分,图中背景方格的边长均为5cm,如果取g=10m/s2,那么:
如图所示为一小球做平抛运动的闪光照相照片的一部分,图中背景方格的边长均为5cm,如果取g=10m/s2,那么: