题目内容
如图所示，长为R的轻质杆（质量不计），一端系一质量为m的小球（球大小不计），绕杆的另一端O在竖直平面内做匀速圆周运动，若小球最低点时，杆对球的拉力大小为1.5mg，求：①小球最低点时的线速度大小？
②小球以多大的线速度运动，通过最高处时杆对球不施力？
分析：（1）小球通过最低点时，由重力和杆的拉力提供向心力，根据向心力公式在最低点列方程可正确求解；
（2）根据最高点重力提供向心力可正确解答．
（2）根据最高点重力提供向心力可正确解答．
解答：解：（1）在最低点由牛顿第二定律得：FT-mg=m
而且：FT=1.5mg
联立解得：v1=
故小球最低点时的线速度大小为：v1=
．
（2）在最高点，只有重力提供向心力：mg=m
解得：v2=
所以当小球以v2=
的速度通过最高点时杆对球无作用力．
| ||
| R |
而且：FT=1.5mg
联立解得：v1=
|
故小球最低点时的线速度大小为：v1=
|
（2）在最高点，只有重力提供向心力：mg=m
| ||
| R |
解得：v2=
| gR |
所以当小球以v2=
| gR |
点评：本题是圆周运动动力学问题，关键是分析物体的受力情况，确定向心力的来源，然后根据向心力公式列方程求解．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，长为R的轻绳，上端固定在O点，下端连一小球．小球接近地面，处于静止状态．现给小球一沿水平方向的初速度v0，小球开始在竖直平面内做圆周运动．设小球到达最高点时绳突然断开．已知小球最后落在离小球最初位置2R的地面上．求：
如图所示，长为R的轻绳一端固定于O点，另一端栓一质量为m的小球，把球拉至最高点A，然后以
如图所示，长为R的轻绳，上端固定在O点，下端连一质量为m的小球．小球接近地面，处于静止状态．现给小球一沿水平方向的初速度v0（未知），小球开始在竖直平面内做圆周运动，小球到达最高点时绳突然断开，小球最后落在离小球最初位置2R远的地面上．设重力加速度为g，空气阻力不计，求：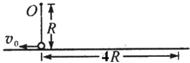
如图所示，长为R的轻绳，上端固定在O点，下端连接一只小球．小球接近地面，处于静止状态．现给小球一沿水平方向的初速度，小球开始在竖直平面内做圆周运动．设小球到达最高点时绳突然断开，已知小球最后落在离小球最初位置4R的地面上，重力加速度为g．试求：（图中所标 v0的数值未知）