题目内容
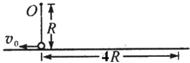 如图所示,长为R的轻绳,上端固定在O点,下端连接一只小球.小球接近地面,处于静止状态.现给小球一沿水平方向的初速度,小球开始在竖直平面内做圆周运动.设小球到达最高点时绳突然断开,已知小球最后落在离小球最初位置4R的地面上,重力加速度为g.试求:(图中所标 v0的数值未知)
如图所示,长为R的轻绳,上端固定在O点,下端连接一只小球.小球接近地面,处于静止状态.现给小球一沿水平方向的初速度,小球开始在竖直平面内做圆周运动.设小球到达最高点时绳突然断开,已知小球最后落在离小球最初位置4R的地面上,重力加速度为g.试求:(图中所标 v0的数值未知)(1)绳突然断开时小球的速度;
(2)小球刚开始运动时,对绳的拉力.
分析:(1)小球在最高点速度沿水平方向,故由平抛运动规律可求得小球的速度;
(2)由机械能守恒可得出小球在最低点的速度;由向心力公式可求得小球对绳子的拉力.
(2)由机械能守恒可得出小球在最低点的速度;由向心力公式可求得小球对绳子的拉力.
解答:解:(1)设绳断后小球以速度v1平抛,则在竖直方向上有:2R=
g t2
在水平方向上有:4R=v1t
解得:v1=2
(2)小球从最低点到最高点过程,小球机械能守恒(选地面为零势能面),有:
m
=mg?2R+
m
合力提供向心力有:F-mg=m
解得:F=9mg
答:(1)绳突然断开时小球的速度为2
;
(2)小球刚开始运动时,对绳的拉力为9mg;
| 1 |
| 2 |
在水平方向上有:4R=v1t
解得:v1=2
| gR |
(2)小球从最低点到最高点过程,小球机械能守恒(选地面为零势能面),有:
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 1 |
合力提供向心力有:F-mg=m
| ||
| R |
解得:F=9mg
答:(1)绳突然断开时小球的速度为2
| gR |
(2)小球刚开始运动时,对绳的拉力为9mg;
点评:本题考查竖直面内的圆周运动,注意小球在运动过程中,只有重力做功,故机械能守恒; 同时小球做圆周运动,需要向心力;故此类问题常常是综合考虑的,要熟练应用其解决方法.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 如图所示,长为R的轻绳,上端固定在O点,下端连一小球.小球接近地面,处于静止状态.现给小球一沿水平方向的初速度v0,小球开始在竖直平面内做圆周运动.设小球到达最高点时绳突然断开.已知小球最后落在离小球最初位置2R的地面上.求:
如图所示,长为R的轻绳,上端固定在O点,下端连一小球.小球接近地面,处于静止状态.现给小球一沿水平方向的初速度v0,小球开始在竖直平面内做圆周运动.设小球到达最高点时绳突然断开.已知小球最后落在离小球最初位置2R的地面上.求: 如图所示,长为R的轻质杆(质量不计),一端系一质量为m的小球(球大小不计),绕杆的另一端O在竖直平面内做匀速圆周运动,若小球最低点时,杆对球的拉力大小为1.5mg,求:
如图所示,长为R的轻质杆(质量不计),一端系一质量为m的小球(球大小不计),绕杆的另一端O在竖直平面内做匀速圆周运动,若小球最低点时,杆对球的拉力大小为1.5mg,求: 如图所示,长为R的轻绳一端固定于O点,另一端栓一质量为m的小球,把球拉至最高点A,然后以
如图所示,长为R的轻绳一端固定于O点,另一端栓一质量为m的小球,把球拉至最高点A,然后以 如图所示,长为R的轻绳,上端固定在O点,下端连一质量为m的小球.小球接近地面,处于静止状态.现给小球一沿水平方向的初速度v0(未知),小球开始在竖直平面内做圆周运动,小球到达最高点时绳突然断开,小球最后落在离小球最初位置2R远的地面上.设重力加速度为g,空气阻力不计,求:
如图所示,长为R的轻绳,上端固定在O点,下端连一质量为m的小球.小球接近地面,处于静止状态.现给小球一沿水平方向的初速度v0(未知),小球开始在竖直平面内做圆周运动,小球到达最高点时绳突然断开,小球最后落在离小球最初位置2R远的地面上.设重力加速度为g,空气阻力不计,求: