题目内容
如图所示,轻杆长2l,中点装在水平轴O点,两端分别固定着小球A和B,A球质量为m ,B球质量为2m,两者一起在竖直平面内绕O轴做圆周运动。
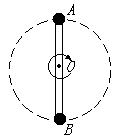
(1)若A球在最高点时,杆A端恰好不受力,求此时O轴的受力大小和方向?
(2)若B球到最高点时的速度等于第(1)小题中A球到达最高点时的速度,则B球运动到最高点时,O轴的受力大小和方向又如何?
(3)在杆的转速逐渐变化的过程中,能否出现O轴不受力的情况?若不能,请说明理由;若能,则求出此时A、B球的速度大小。

(1)若A球在最高点时,杆A端恰好不受力,求此时O轴的受力大小和方向?
(2)若B球到最高点时的速度等于第(1)小题中A球到达最高点时的速度,则B球运动到最高点时,O轴的受力大小和方向又如何?
(3)在杆的转速逐渐变化的过程中,能否出现O轴不受力的情况?若不能,请说明理由;若能,则求出此时A、B球的速度大小。
(1)4mg,方向竖直向下(2)2mg,方向竖直向下(3)能 

试题分析:(1)A在最高点时,对A有
 ,对B有
,对B有 ,可得
,可得 。根据牛顿第三定律,O轴所受有力大小为4mg,方向竖直向下
。根据牛顿第三定律,O轴所受有力大小为4mg,方向竖直向下(2)B在最高点时,对B有
 ,代入(1)中的v,可得
,代入(1)中的v,可得 ;
;对A有
 ,
, 。根据牛顿第三定律,O轴所受的力的大小为2mg,方向竖直向下
。根据牛顿第三定律,O轴所受的力的大小为2mg,方向竖直向下(3)要使O轴不受力,据B的质量大于A的质量,可判断B球应在最高点。对B有
 ,对A有
,对A有 。轴O不受力时,
。轴O不受力时, ,
,可得
 ,所以
,所以
点评:竖直平面内的圆周运动的规律是
 ,要认真分析个物体的受力情况,并抓住两物体线速度相等这一重要特点。
,要认真分析个物体的受力情况,并抓住两物体线速度相等这一重要特点。
练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目

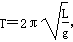 求它们通过竖直位置时杆分别对上下两球的作用力,并说明是拉力还是支 持力.
求它们通过竖直位置时杆分别对上下两球的作用力,并说明是拉力还是支 持力.




 ,过凸桥最高点时,对桥的压力是车重的一半,则桥面的曲率半径为_______
,过凸桥最高点时,对桥的压力是车重的一半,则桥面的曲率半径为_______ ,当车速为______
,当车速为______ ,车对桥面最高点的压力恰好为零.g取10m/s2
,车对桥面最高点的压力恰好为零.g取10m/s2




