题目内容
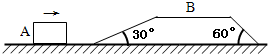 如图所示,一个横截面为梯形,质量为4kg的木块B静止置于水平光滑的地面上,木块的两个斜面均光滑,倾角分别为30°、60°;木块的上底面为水平的粗糙面,其长度为1.4m,上底面距地面的高度为9/25m.现质量为 1kg的木块A(可视为质点)以速度v0沿水平光滑地面向木块B滑去.(木块A与木块B上底面之间的滑动摩擦系数为0.2;木块B的两个斜面与上、下底面的交界处为圆弧面,g取10m/s2).试讨论:(1)当木块A的速度v0=2m/s时,木块A、B的最终运动情况;
如图所示,一个横截面为梯形,质量为4kg的木块B静止置于水平光滑的地面上,木块的两个斜面均光滑,倾角分别为30°、60°;木块的上底面为水平的粗糙面,其长度为1.4m,上底面距地面的高度为9/25m.现质量为 1kg的木块A(可视为质点)以速度v0沿水平光滑地面向木块B滑去.(木块A与木块B上底面之间的滑动摩擦系数为0.2;木块B的两个斜面与上、下底面的交界处为圆弧面,g取10m/s2).试讨论:(1)当木块A的速度v0=2m/s时,木块A、B的最终运动情况;(2)当木块A的速度v0=3.6m/s时,木块A、B的最终运动情况.
分析:把木块A和木块B看做一个系统,系统动量守恒,
由于木块A与木块B上底面之间有摩擦,应用动量守恒定律分别求出最左端和最右端的共同速度.
根据题目中提供的速度进行讨论,确定研究的过程,再应用动量守恒和能量守恒结合解决问题.
由于木块A与木块B上底面之间有摩擦,应用动量守恒定律分别求出最左端和最右端的共同速度.
根据题目中提供的速度进行讨论,确定研究的过程,再应用动量守恒和能量守恒结合解决问题.
解答:解:设木块质量分别为mA、mB木块B的高为h,上底面长为L,
这里有两种临界状态:
①当木块A刚滑上木块B上底面的最左端时,木块A、B具有共同的速度v1′,
设此时木块A的初速度为v1,则有:mAv1=(mA+mB)v1′
mAv12=
(mA+mB)v1 2+mAgh
解得:v1=3m/s
②当木块A刚滑到木块B的最右端时,木块A、B具有共同的速度v2′
设此时木块A的初速度为v2,则有:mAv2=(mA+mB)v2′
mAv22=
(mA+mB)v2 2+mAgh+μmAgL
解之得:v2=4m/s
(1)当v0=2m/s<v1=3m/s时,木块A不能滑上木块B的上底面,相当于A、B发生了弹性碰撞.
设碰撞后木块A、B的速度分别为vA、vB
则有:vA=
vB=
解之得;vA=-1.2m/s; vB=0.8m/s;
即木块A、B的最终运动情况是:木块A以1.2m/s的速度向左运动,木块B以0.8m/s的速度向右运动.
(2)当v0=3.6m/s<v2=4m/s时,木块A能滑上木块B的上底面,但不能滑到其最右端,
此时木块A、B具有共同向右的速度v.
设木块A在木块B的上底面上滑行距离为S,则有:mAv0=(mB+mA)v
mAv02=
(mB+mA)v2+mAgh+μmAgS
解之得:v=0.72m/s (S=0.8m)
即木块A、B最终以共同的速度v=0.72m/s向右运动.
答:(1)当v0=2m/s,木块A以1.2m/s的速度向左运动,木块B以0.8m/s的速度向右运动.
(2)当v0=3.6m/s木块A、B最终以共同的速度v=0.72m/s向右运动.
这里有两种临界状态:
①当木块A刚滑上木块B上底面的最左端时,木块A、B具有共同的速度v1′,
设此时木块A的初速度为v1,则有:mAv1=(mA+mB)v1′
| 1 |
| 2 |
| 1 |
| 2 |
解得:v1=3m/s
②当木块A刚滑到木块B的最右端时,木块A、B具有共同的速度v2′
设此时木块A的初速度为v2,则有:mAv2=(mA+mB)v2′
| 1 |
| 2 |
| 1 |
| 2 |
解之得:v2=4m/s
(1)当v0=2m/s<v1=3m/s时,木块A不能滑上木块B的上底面,相当于A、B发生了弹性碰撞.
设碰撞后木块A、B的速度分别为vA、vB
则有:vA=
| (mA-mB)v0 |
| mB+mA |
vB=
| 2mAv0 |
| mB+mA |
解之得;vA=-1.2m/s; vB=0.8m/s;
即木块A、B的最终运动情况是:木块A以1.2m/s的速度向左运动,木块B以0.8m/s的速度向右运动.
(2)当v0=3.6m/s<v2=4m/s时,木块A能滑上木块B的上底面,但不能滑到其最右端,
此时木块A、B具有共同向右的速度v.
设木块A在木块B的上底面上滑行距离为S,则有:mAv0=(mB+mA)v
| 1 |
| 2 |
| 1 |
| 2 |
解之得:v=0.72m/s (S=0.8m)
即木块A、B最终以共同的速度v=0.72m/s向右运动.
答:(1)当v0=2m/s,木块A以1.2m/s的速度向左运动,木块B以0.8m/s的速度向右运动.
(2)当v0=3.6m/s木块A、B最终以共同的速度v=0.72m/s向右运动.
点评:本题较复杂些,首先要正确的判断两滑块的相对位置,再根据题目要求进行列等式解决.

练习册系列答案
相关题目
 如图所示,一个横截面为直角三角形的三棱镜,∠A=30°,∠O=90°.三棱镜材料的折射率是n=
如图所示,一个横截面为直角三角形的三棱镜,∠A=30°,∠O=90°.三棱镜材料的折射率是n= 如图所示,一个横截面为直角三角形的三棱镜,∠A=30°,∠C=90°.三棱镜材料的折射率是.一束与BC面成θ=30°角的光线射向BC面.
如图所示,一个横截面为直角三角形的三棱镜,∠A=30°,∠C=90°.三棱镜材料的折射率是.一束与BC面成θ=30°角的光线射向BC面. 如图所示,一个横截面为直角三角形的三棱镜,∠A=30°,∠C=90°.三棱镜材料的折射率是 n=
如图所示,一个横截面为直角三角形的三棱镜,∠A=30°,∠C=90°.三棱镜材料的折射率是 n= 如图所示,一个横截面为直角三角形的三棱镜,∠A=30°,∠C=90°,BC边的长为L.一个大光屏MN与BC平行,到BC的距离也是L.三棱镜材料的折射率是
如图所示,一个横截面为直角三角形的三棱镜,∠A=30°,∠C=90°,BC边的长为L.一个大光屏MN与BC平行,到BC的距离也是L.三棱镜材料的折射率是