题目内容
7.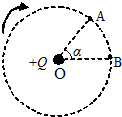 如图,两质量均为m、电荷量分别为q、2q的带负电粒子A、B在同一圆周上绕位于圆心O点的点电荷+Q做顺时针方向、半径为R的匀速圆周运动,A、B所在半径间的夹角为α.不计彼此间的万有引力以及A、B间的库仑力.已知静电力常量为k.求:
如图,两质量均为m、电荷量分别为q、2q的带负电粒子A、B在同一圆周上绕位于圆心O点的点电荷+Q做顺时针方向、半径为R的匀速圆周运动,A、B所在半径间的夹角为α.不计彼此间的万有引力以及A、B间的库仑力.已知静电力常量为k.求:(1)粒子A绕O点做圆周运动的动能;
(2)粒子B绕O点做圆周运动的周期;
(3)经过多少时间粒子A、B第一次相遇.
分析 (1、2)根据牛顿第二定律,结合引力提供向心力,即可求解;
(3)根据以上所求得周期表达式,结合B必须比A多绕(2π-α),才能追上A,从而即可求解.
解答 解:(1)根据引力提供向心力,由牛顿第二定律,则有:$\frac{kQq}{{R}^{2}}=m\frac{{v}_{A}^{2}}{R}$
解得:EKA=$\frac{1}{2}{mv}_{A}^{2}$=$\frac{KQq}{2R}$;
(2)根据引力提供向心力,则有:$\frac{KQ•2q}{{R}^{2}}=m\frac{4{π}^{2}}{{T}_{B}^{2}}R$
解得:TB=2π$\sqrt{\frac{m{R}^{3}}{2kQq}}$;
(3)同理,根据引力提供向心力,则有:TA=2π$\sqrt{\frac{m{R}^{3}}{kQq}}$,
由题意可知,B必须比A多绕(2π-α),才能追上A;
因此(2π-α)=(ωB-ωA)•△t;
根据$ω=\frac{2π}{T}$,可得:(2π-α)=($\frac{2π}{{T}_{B}}-\frac{2π}{{T}_{A}}$)△t.
解得:△t=$\frac{(2π-α)}{\sqrt{2}-1}\sqrt{\frac{m{R}^{3}}{kQq}}$;
答:(1)粒子A绕O点做圆周运动的动能$\frac{KQq}{2R}$;
(2)粒子B绕O点做圆周运动的周期2π$\sqrt{\frac{m{R}^{3}}{2kQq}}$;
(3)经过多少时间粒子A、B第一次相遇$\frac{(2π-α)}{\sqrt{2}-1}\sqrt{\frac{m{R}^{3}}{kQq}}$.
点评 考查牛顿第二定律的应用,掌握万有引力定律与向心力表达式的内容,注意当能相遇时,B比A多绕多少角度是解题的关键.

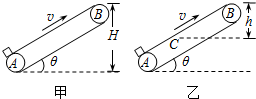 如图所示,甲、乙两传送带与水平面的夹角相同,都以恒定速率v向上运动.现将一质量为m的小物体(视为质点)轻轻放在A处,小物体在甲传送带上到达B处时恰好达到传送带的速率v;在乙传送带上到达离B处竖直高度为h的C处时达到传送带的速率v,已知B处离地面的高度均为H.则在小物体从A到B的过程中( )
如图所示,甲、乙两传送带与水平面的夹角相同,都以恒定速率v向上运动.现将一质量为m的小物体(视为质点)轻轻放在A处,小物体在甲传送带上到达B处时恰好达到传送带的速率v;在乙传送带上到达离B处竖直高度为h的C处时达到传送带的速率v,已知B处离地面的高度均为H.则在小物体从A到B的过程中( )| A. | 小物体与甲传送带间的动摩擦因数较小 | |
| B. | 两传送带对小物体做功相等 | |
| C. | 两传送带消耗的电能相等 | |
| D. | 两种情况下因摩擦产生的热量相等 |
| A. | 电场强度 | B. | 电势 | C. | 电势能 | D. | 电势差 |
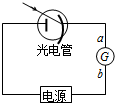
| A. | 电源右端应为正极 | |
| B. | 流过电流表G的电流大小取决于照射光的频率 | |
| C. | 流过电流表G的电流方向是a流向b | |
| D. | 普朗克解释了光电效应并提出光子能量E=hν |
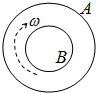 如图,两同心圆环A、B置于同一水平面上,其中B为均匀带负电绝缘环,A为导体环.当B绕轴心顺时针转动且转速增大.下列说法正确的是( )
如图,两同心圆环A、B置于同一水平面上,其中B为均匀带负电绝缘环,A为导体环.当B绕轴心顺时针转动且转速增大.下列说法正确的是( )| A. | A中产生逆时针的感应电流 | B. | A中产生顺时针的感应电流 | ||
| C. | A具有收缩的趋势 | D. | A具有扩展的趋势 |
 如图所示,电阻不计、相距L的两条足够长的平行金属导轨倾斜放置,与水平面的夹角vm,整个空间存在垂直于导轨平面的匀强磁场,磁感应强度为B,导轨上固定有质量为m,电阻为R的两根相同的导体棒,导体棒MN上方轨道粗糙下方光滑,将两根导体棒同时释放后,观察到导体棒MN下滑而EF始终保持静止,当MN下滑的距离为S时,速度恰好达到最大值Vm,则下列叙述正确的是( )
如图所示,电阻不计、相距L的两条足够长的平行金属导轨倾斜放置,与水平面的夹角vm,整个空间存在垂直于导轨平面的匀强磁场,磁感应强度为B,导轨上固定有质量为m,电阻为R的两根相同的导体棒,导体棒MN上方轨道粗糙下方光滑,将两根导体棒同时释放后,观察到导体棒MN下滑而EF始终保持静止,当MN下滑的距离为S时,速度恰好达到最大值Vm,则下列叙述正确的是( )| A. | 导体棒MN的最大速度Vm=$\frac{2mgRsinθ}{{B}^{2}{L}^{2}}$ | |
| B. | 此时导体棒EF与轨道之间的静摩擦力为mgsinθ | |
| C. | 当导体棒MN从静止开始下滑S的过程中,通过其横截面的电荷量为$\frac{BLS}{2R}$ | |
| D. | 当导体棒MN从静止开始下滑S的过程中,导体棒MN中产生的热量为mgSsinθ-$\frac{1}{2}$mVm2 |

| A. | 0~4s合外力一直对物体做正功 | |
| B. | 2s~5s物体受到的合外力方向不变 | |
| C. | 2s~5s物体所受合外力方向与运动方向相反 | |
| D. | 第1秒内与第6秒内物体所受合外力方向相反 |
| A. | 布朗运动就是液体分子的热运动 | |
| B. | 将大颗粒的盐磨成细盐,就变成了非晶体 | |
| C. | 第二类永动机虽然不违反能量守恒定律,但它是制造不出来的 | |
| D. | 在绝热条件下压缩气体,气体的内能一定增加 |
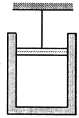 如图所示,一圆柱形气缸质量M为10kg,总长度L为40cm,内有一活塞,质量m为5kg,截面积S为50cm2,活塞与气缸壁间摩擦可忽略,但不漏气(不计气缸壁与活塞厚度).用绳子系住活塞将气缸悬挂起来,外界大气压强p0为1×l05Pa,当温度t0为7℃时,气缸内气体柱的高L1为35cm,g取10m/s2.求:
如图所示,一圆柱形气缸质量M为10kg,总长度L为40cm,内有一活塞,质量m为5kg,截面积S为50cm2,活塞与气缸壁间摩擦可忽略,但不漏气(不计气缸壁与活塞厚度).用绳子系住活塞将气缸悬挂起来,外界大气压强p0为1×l05Pa,当温度t0为7℃时,气缸内气体柱的高L1为35cm,g取10m/s2.求: