题目内容
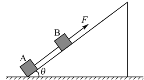
【题目】如图，一劲度系数为k轻弹簧的一端固定在倾角为θ=30°的光滑固定斜面的底部，另一端和质量为2m的小物块A相连，质量为m的物块B紧靠A一起静止.现用手缓慢斜向下压物体B使弹簧再压缩x0并静止。然后迅速放手， A和B一起沿斜面向上运动距离L时， B达到最大速度v．则以下说法正确的是(始终在弹性限度内)
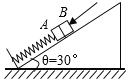
A. L>x0
B. 放手的瞬间，A对B的弹力大小为
+
C. 若向上运动过程A、B出现了分离，则分离时弹簧的压缩量为
D. 从放手到“A和B达到最大速度v”的过程中，弹簧弹性势能减小了
【答案】B
【解析】
A：设物块B紧靠A一起静止时弹簧的压缩量为
，对整体受力分析由平衡条件可得：
；设B达到最大速度v时，弹簧的压缩量为
，B达到最大速度v时，AB一起向上运动，加速度均为零，对整体受力分析可得：
；解得：
，则整体先下移x0，再向上运动距离L时，弹簧形变量相同，即
。故A项错误。
B：放手瞬间，弹簧压缩量为
，对整体受力分析由牛顿第二定律可得：
；对物块B受力分析由牛顿第二定律可得：
，解得：
。故B项正确。
C：若向上运动过程A、B出现分离时，A、B间力恰为零，且此时A、B加速度相同。对B受力分析由牛顿第二定律可得：
，对A受力分析由牛顿第二定律可得：
，解得：
，则分离时弹簧的压缩量为0。故C项错误。
D：从放手到“A和B达到最大速度v”的过程中，AB及弹簧组成的系统机械能守恒，弹簧弹性势能减小等于AB重力势能和动能的增量，则
。故D项错误。
练习册系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
期末复习检测系列答案
相关题目
