题目内容
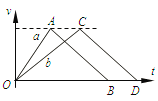
【题目】从某一高度相隔1s先后释放两个相同的小球甲和乙，不计空气阻力，它们在空中任一时刻（ ）
A.甲乙两球距离始终保持不变，甲乙两球速度之差保持不变
B.甲乙两球距离越来越大，甲乙两球速度之差也越来越大
C.甲乙两球距离越来越大，甲乙两球速度之差保持不变
D.甲乙两球距离越来越小，甲乙两球速度之差也越来越小
【答案】C
【解析】解：设乙运动的时间为t，则甲运动时间为t+1，
则两球的距离x= 
﹣ 
=gt+ 
，可见，两球间的距离随时间推移，越来越大．
两球速度之差为：△v=g（t+1）﹣gt=g，所以甲乙两球速度之差保持不变．
所以C选项正确．
故ABD不符合题意，C符合题意。
所以答案是：C．
【考点精析】解答此题的关键在于理解自由落体运动的相关知识，掌握（1）条件:初速度为零，只受重力作用；（2）性质:是一种初速为零的匀加速直线运动，a=g．
【题目】学校开展研究性学习，某同学为了探究杆子转动时的动能表达式，设计了下图甲所示的实验：质量为m的均匀长直杆一端固定在转轴O处，杆由水平位置静止释放，用置于圆弧上某位置的光电门测出另一端A经过该位置时的瞬时速度vA，并记下该位置与转轴O的高度差h．
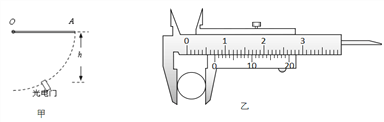
⑴该同学用20分度的游标卡尺测得长直杆的横截面的直径如图乙为______________mm．
⑵调节光电门在圆弧上的位置，测得多组数据如表格所示．请选择适当的数据处理方法，猜想并写出vA与h的函数关系等式___________________.
组次 | 1 | 2 | 3 | 4 | 5 |
h/m | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 |
vA（m/s） | 1.73 | 2.12 | 2.46 | 2.74 | 3.00 |
⑶当地重力加速度g取10m/s2，不计一切摩擦，结合你找出的函数关系式，根据守恒规律写出此杆转动时动能的表达式EK= ________（请用数字、质量m、速度vA表示）.
