题目内容
5. 如图所示,绷紧的水平传送带足够长,始终以v1=2m/s的恒定速率运行.初速度大小为v2=3m/s的小墨块从与传送带等高的光滑水平面上的A处滑上传进带.若从小墨块滑上传送带开始计时,小墨块在传送带上运动5s后与传送带的速度相同,求:
如图所示,绷紧的水平传送带足够长,始终以v1=2m/s的恒定速率运行.初速度大小为v2=3m/s的小墨块从与传送带等高的光滑水平面上的A处滑上传进带.若从小墨块滑上传送带开始计时,小墨块在传送带上运动5s后与传送带的速度相同,求:(1)小墨块向左运动的最远距离,
(2)小墨块在传送带上留下的痕迹长度.
分析 (1)分析小墨块的受力及运动情况,根据运动学公式可求得加速度,再由运动学公式可求得小墨块前进的位移;
(2)分析小墨块及传送带的运动,只有要二者有相对运动,就会在传送带上形成痕迹;求出相对静止的时间,再由运动学公式求出各自的位移,即可求得痕迹长度.
解答 解:(1)设向右为正方向,小墨块速度未与传送带速度相同时,受到的摩擦力始终向右,加速度始终向右,根据运动学知识可知:
a=$\frac{△v}{△t}$=$\frac{2-(-3)}{5}$=1m/s2;
小墨块向左减速运动时,对小墨块有:
0=v2-at1
x1=$\frac{0+{v}_{2}}{2}$t1
联立解得:x1=4.5m;
(2)小墨块向左减速的过程中,对传送带的位移为:
x2=v1t1
小墨块向右加速运动时,对小墨块有:
v1=at2
x1′=$\frac{0+{v}_{1}}{2}{t}_{2}$
对传送带x2'=v1t2
因而小墨块在传送带上的痕迹长度为:
x=(x1+x2)+(x2′-x1′)
解得:x=12.5m;
答:(1)小墨块向左运动的最远距离为4.5m;
(2)小墨块在传送带上留下的痕迹长度为12.5m.
点评 本题考查传送带问题中运动学公式的应用,要注意正确分析二者间的联系,分别由位移公式及速度公式进行分析求解;注意小墨块有返回过程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.“轨道电子俘获”也是放射性同位素衰变的一种形式,它是指原子核(称为母核)俘获一个核外电子,其内部一个质子变为中子,从而变成一个新核(称为子核),并且放出一个中微子的过程,中微子的质量极小,不带电,很难被探测到,人们最早是通过子核的反冲而间接证明中微子的存在的.关于一个静止的母核发生“轨道电子俘获”,衰变为子核并放出中微子,下面的说法中正确的是( )
| A. | 子核的动量与中微子的动量大小相同 | |
| B. | 母核的电荷数小于子核的电荷数 | |
| C. | 母核的质量数等于子核的质量数 | |
| D. | 子核的动能大于中微子的动能 |
13.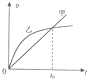 质量相等的甲乙两物体从离地面相同高度同时由静止开始下落,由于两物体的形状不同,运动中受到的空气阻力不同.将释放时刻作为t=0时刻,两物体的v-t图象如图所示.则下列判断正确的是( )
质量相等的甲乙两物体从离地面相同高度同时由静止开始下落,由于两物体的形状不同,运动中受到的空气阻力不同.将释放时刻作为t=0时刻,两物体的v-t图象如图所示.则下列判断正确的是( )
 质量相等的甲乙两物体从离地面相同高度同时由静止开始下落,由于两物体的形状不同,运动中受到的空气阻力不同.将释放时刻作为t=0时刻,两物体的v-t图象如图所示.则下列判断正确的是( )
质量相等的甲乙两物体从离地面相同高度同时由静止开始下落,由于两物体的形状不同,运动中受到的空气阻力不同.将释放时刻作为t=0时刻,两物体的v-t图象如图所示.则下列判断正确的是( )| A. | t0时刻之前,甲物体受到的空气阻力总是大于乙物体受到的空气阻力 | |
| B. | 甲物体在t0时刻的速度小于乙物体0-t0时间内的平均速度 | |
| C. | t0时刻甲乙两物体在同一高度 | |
| D. | 两物体不可能同时落地 |
20. 如图所示,质量均为1kg的小球a、b在轻弹簧A、B及外力F的作用下处于平衡状态,其中A、B两个弹簧劲度系数均为5N/cm,B弹簧上端与天花板固定连接,轴线与竖直方向的夹角为60°,A弹簧竖直,g取10m/s2,则以下说法正确的是( )
如图所示,质量均为1kg的小球a、b在轻弹簧A、B及外力F的作用下处于平衡状态,其中A、B两个弹簧劲度系数均为5N/cm,B弹簧上端与天花板固定连接,轴线与竖直方向的夹角为60°,A弹簧竖直,g取10m/s2,则以下说法正确的是( )
 如图所示,质量均为1kg的小球a、b在轻弹簧A、B及外力F的作用下处于平衡状态,其中A、B两个弹簧劲度系数均为5N/cm,B弹簧上端与天花板固定连接,轴线与竖直方向的夹角为60°,A弹簧竖直,g取10m/s2,则以下说法正确的是( )
如图所示,质量均为1kg的小球a、b在轻弹簧A、B及外力F的作用下处于平衡状态,其中A、B两个弹簧劲度系数均为5N/cm,B弹簧上端与天花板固定连接,轴线与竖直方向的夹角为60°,A弹簧竖直,g取10m/s2,则以下说法正确的是( )| A. | A弹簧伸长量为3cm | B. | 外力F=10$\sqrt{3}$N | ||
| C. | B弹簧的伸长量为4cm | D. | 突然撤去外力F瞬间,b球加速度为0 |
10. 如图所示,空间中存在一匀强磁场,将长度为L的直导线放置在y轴上,当通以大小为I、沿y轴负方向的电流后,测得其受到的安培力大小为F.方向沿x轴正方向.则关于的磁感应强度的方向和大小,说法正确的是( )
如图所示,空间中存在一匀强磁场,将长度为L的直导线放置在y轴上,当通以大小为I、沿y轴负方向的电流后,测得其受到的安培力大小为F.方向沿x轴正方向.则关于的磁感应强度的方向和大小,说法正确的是( )
 如图所示,空间中存在一匀强磁场,将长度为L的直导线放置在y轴上,当通以大小为I、沿y轴负方向的电流后,测得其受到的安培力大小为F.方向沿x轴正方向.则关于的磁感应强度的方向和大小,说法正确的是( )
如图所示,空间中存在一匀强磁场,将长度为L的直导线放置在y轴上,当通以大小为I、沿y轴负方向的电流后,测得其受到的安培力大小为F.方向沿x轴正方向.则关于的磁感应强度的方向和大小,说法正确的是( )| A. | 只能沿x轴正方向 | B. | 可能在xOz平面内,大小为$\frac{2F}{IL}$ | ||
| C. | 可能在xOy平面内,大小为$\frac{2F}{IL}$ | D. | 可能在zOy平面内,大小为$\frac{2F}{IL}$ |
17.2014年我国多地都出现了雾霾天气,严重影响了人们的健康和交通.设有一辆汽车在能见度较低的雾霾天气里以54km/h的速度匀速行驶,司机突然看到正前方有一辆静止的故障车,该司机刹车的反应时间为0.6s,刹车后汽车匀减速前进,刹车过程中加速度大小为5m/s2,最后停在故障车前1.5m处,避免了一场事故.以下说法正确的是( )
| A. | 司机发现故障车后,汽车经过3 s停下 | |
| B. | 司机发现故障车时,汽车与故障车的距离为33 m | |
| C. | 从司机发现故障车到停下来的过程,汽车的平均速度为7.5 m/s | |
| D. | 从司机发现故障车到停下来的过程,汽车的平均速度为11 m/s |
14.如图所示,一质量为M的木板静止在光滑的水平面上,一质量为m的滑块以初速度v0滑到木板上,滑块在木板上滑行的距离为d,木板向前移动x后以速度v与滑块一起匀速运动,此过程中转化为内能的能量为( )


| A. | $\frac{1}{2}$m(v02-v0v) | B. | mv0(v0-v) | C. | $\frac{m({v}_{0}-v)vd}{2x}$ | D. | $\frac{m({v}_{0}-v)}{x}vd$ |
 如图甲,光滑竖直固定的杆上套有下端接触地面的轻弹簧和一个小物体.将小物体从一定高度处由静止释放,通过传感器测量出小物体的速度及对应离地高度h,作出其动能Ek与高度h的图象如图乙.其中,高度在0.6m~0.8m范围内图象为直线,其余部分为曲线.以地面为零势能面,g取10m/s2.求
如图甲,光滑竖直固定的杆上套有下端接触地面的轻弹簧和一个小物体.将小物体从一定高度处由静止释放,通过传感器测量出小物体的速度及对应离地高度h,作出其动能Ek与高度h的图象如图乙.其中,高度在0.6m~0.8m范围内图象为直线,其余部分为曲线.以地面为零势能面,g取10m/s2.求