题目内容
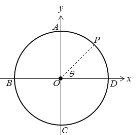
【题目】如图所示,竖直平面内四分之一光滑圆弧轨道AP和水平传送带PC相切于P点,圆弧轨道的圆心为O,半径为R.一质量为m的小物块从圆弧顶点A由静止开始沿轨道下滑,再滑上传送带PC,传送带可以速度![]() 沿逆时针方向的传动.小物块与传送带间的动摩擦因数为μ,不计物体经过圆弧轨道与传送带连接处P时的机械能损失,若传送带沿逆时针方向转动,物块恰能滑到右端C,重力加速度为g=10 m/s2.则下列说法正确的是
沿逆时针方向的传动.小物块与传送带间的动摩擦因数为μ,不计物体经过圆弧轨道与传送带连接处P时的机械能损失,若传送带沿逆时针方向转动,物块恰能滑到右端C,重力加速度为g=10 m/s2.则下列说法正确的是

A. 若水平传送带沿逆时针方向转动的速度增大,小物块不能滑到传送带右端C
B. 传送带PC之间的距离![]()
C. 若传送带速度大小v0不变,顺时针转动,小物块从P点滑到C点所用的时间![]()
D. 若传送带速度大小v0不变,顺时针转动,要让小物块一直在传送带上做匀减速运动,则小物块在圆弧顶点A的最小速度![]()
【答案】BCD
【解析】
传送带沿逆时针方向转动时,物体在传送带上受到的滑动摩擦力与转速无关,运动情况不变。从A到C对小物块运用动能定理列式,可求得PC之间的距离L;若传送带速度大小v0不变,顺时针转动,先由动能定理求出物块到达P点的速度。分析物块滑上传送带后的运动情况,由牛顿第二定律和运动学公式求物块从P点滑到C点所用的时间t;若传送带速度大小v0不变,要让小物块一直在传送带上做匀减速运动,则小物块滑到传送带右端C时速度恰好与传送带共速,再由运动学公式和动能定理求解小物块在圆弧顶点A的最小速度。
A、若水平传送带沿逆时针方向转动的速度增大,物块受到的滑动摩擦力不变,滑动摩擦力做功与速度变大前一样,故小物块仍然恰能滑到右端C,故A错误;
B、从A到C,对小物块运用动能定理可得:![]() ,解得:
,解得:![]() ,故B正确;
,故B正确;
C、若传送带速度大小v0不变,顺时针转动,根据动能定理得:![]() ,可得,物块滑动到P点的速度:
,可得,物块滑动到P点的速度:![]()
根据牛顿第二定律可得:![]() ,得
,得 ![]()
假设传送带足够长,共速时间:![]()
共速时小物块相对P点向右运动的位移:![]() ,故小物块在传送带上先做匀减速运动,然后做匀速运动,则匀速运动的时间为:
,故小物块在传送带上先做匀减速运动,然后做匀速运动,则匀速运动的时间为: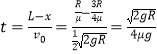
可得小物块从P点滑到C点所用的时间:![]() ,故C正确;
,故C正确;
D、若传送带速度大小v0不变,要让小物块一直在传送带上做匀减速运动,则小物块滑到传送带右端C时速度恰好与传送带共速为:![]()
对整个过程,由动能定理得:![]()
解得![]() ,即小物块在圆弧顶点A的最小速度
,即小物块在圆弧顶点A的最小速度![]() ,故D正确。
,故D正确。

【题目】在研究平抛运动的实验中,某同学记录了小球运动途中经过的A、B、C、D、E、F、G点的位置,相邻两点的时间间隔均为![]() =0.05s。取A点为坐标原点,以+x方向表示水平初速度方向、+y方向表示竖直向下方向,实验记录如下:(结果保留两位小数)
=0.05s。取A点为坐标原点,以+x方向表示水平初速度方向、+y方向表示竖直向下方向,实验记录如下:(结果保留两位小数)
标号n | A | B | C | D | E | F | G |
t(s) | 0 | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 |
x(m) | 0 | 0.024 | 0.051 | 0.073 | 0.098 | 0.126 | 0.150 |
y(m) | 0 | 0.042 | 0.108 | 0.198 | 0.314 | 0.454 | 0.617 |

(1)作出x—t图象如图1所示,小球平抛运动的水平初速度大小是______m/s;
(2)以t为横坐标,![]() 为纵坐标,作出
为纵坐标,作出![]() —t图象如图2所示,其函数解析式为
—t图象如图2所示,其函数解析式为![]() = 4.88t + 0.59:
= 4.88t + 0.59:
①重力加速度的测量值是________m/s;
②t=0.10s时,小球的竖直分速度大小是_________m/s;