题目内容
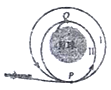
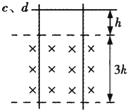
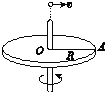
【题目】如图，半径为R的水平圆盘绕过圆心O的竖直轴匀速转动，A为圆盘边缘上一点．某时刻，在O的正上方有一个可视为质点的小球以初速度v沿半径OA方向水平抛出，若小球恰好直接落在A点，重力加速度为g，则（ ）
A. 小球从抛出到落在A点的时间为
B. 小球抛出时距O的高度为
C. 圆盘转动的最小角速度为
D. 圆盘转动的角速度可能等于
【答案】BCD
【解析】
小球做平抛运动，小球在水平方向上做匀速直线运动，在竖直方向做自由落体运动，根据水平位移求出运动的时间，根据竖直方向求出高度．圆盘转动的时间和小球平抛运动的时间相等，在这段时间内，圆盘转动n圈，写出角速度的通项，再求出角速度的最小值和可能值．
小球做平抛运动，小球在水平方向上做匀速直线运动，则平抛运动的时间t=
；竖直方向做自由落体运动，则小球抛出时距O的高度h=
；根据ωt=2nπ得：圆盘转动的角速度ω=
（n=1、2、3…）；当n=1时，圆盘转动的最小角速度为
；当n=2时，圆盘转动的角速度等于
．故A错误，BCD正确．故选BCD.
练习册系列答案
相关题目
