��Ŀ����
 ��1��Ϊ�˽��������Դ֮�裬ʵ���ú��ܴ���ú��ʯ�͵Ȳ���������Դ���ܶ���Ҷ�������ȫ�����˾۱䡰����̫���������ǴӺ�ˮ����ȡԭ�ϣ������ڶȵĸ����·����Ŀɿغ˾۱䷴Ӧ����ѧ�����ݵĺ˷�Ӧ������
��1��Ϊ�˽��������Դ֮�裬ʵ���ú��ܴ���ú��ʯ�͵Ȳ���������Դ���ܶ���Ҷ�������ȫ�����˾۱䡰����̫���������ǴӺ�ˮ����ȡԭ�ϣ������ڶȵĸ����·����Ŀɿغ˾۱䷴Ӧ����ѧ�����ݵĺ˷�Ӧ������A
A
��A��21H+31H��42He+10n
B��92235U+01n��14156Ba+9236Kr+301n
C��90234Th��91234Pa+-10e
D��92238U��90234Th+24He
��2����ԭ�ӵ�n�ܼ�������ΪEn=
| E1 |
| n2 |
| 3 |
| 16 |
| 3 |
| 4 |
4
4
�ܼ���������Ӻ��ڵ�2
2
�ܼ�����3����ͼ��ʾ������A��B�������ֱ�Ϊm1��m2�������ʵ������������ڹ⻬ˮƽ���ϣ������������������ʹ���ɴ������ѹ��״̬����һ���������������һ���Ժ㶨������v0���һ�������ͻȻ�Ͽ������������ɵ�һ�λָ�ԭ��ʱ������A�Ķ��ܱ�Ϊԭ����
| 1 |
| 4 |
��������1���˹��Ⱥ˾۱������������϶ȵĸ��������£��������ͬλ��뮡�밵ĺ˾۱䣮��Ӧ�������������������Ⱦ�ĺ������ڷ�Ӧ���¶ȸߣ��ͷų����ĺ��ܶ࣬�׳ơ�����̫������
��2������õ�������Ӻ���ԭ������ΪE=E1+��-
E1��=
��������ԭ�ӵ�n�ܼ�������ΪEn=
������n����ֵ���жϷ�����Ӻ���ԭ���������ܼ������ݲ���������ԭ�ӷ����������E=Em-En��m��n�����õ���ԭ�ӷ������ǰ���������ж��ܼ���
��3��ϸ�߶Ͽ����ɻָ�ԭ��ǰ�����ɶ�A��B��������ĵ����������B���٣�����A���ٲ��ҷ�����ٵ����ܱ�Ϊ
���������⣬���A������ܵ��ٶȣ�Ȼ����ݶ����غ㶨����ʽ�����ʵ��������з�����
��2������õ�������Ӻ���ԭ������ΪE=E1+��-
| 3 |
| 4 |
| E1 |
| 4 |
| E1 |
| n2 |
��3��ϸ�߶Ͽ����ɻָ�ԭ��ǰ�����ɶ�A��B��������ĵ����������B���٣�����A���ٲ��ҷ�����ٵ����ܱ�Ϊ
| 1 |
| 4 |
����⣺��1���˹��Ⱥ˾۱������������϶ȵĸ��������£��������ͬλ��뮡�밵ĺ˾۱䣮��Ӧ�������������������Ⱦ�ĺ�����ѡA
��2������õ�������Ӻ���ԭ������ΪE=E1+��-
E1��=
�����ݲ���������ԭ�ӷ����������E=Em-En��m��n�����õ���ԭ�ӷ������ǰ������E��=
+��-
E1��=
��������ԭ�ӵ�n�ܼ�������ΪEn=
���õ��������ǰn=4��������Ӻ�n=2��
��3��A���鶯��Ϊ��̬��
���軬��A��ʱ����Ϊv��B������ٶ�ΪvB
��A������
mv02=
?
mv2
��ã�v=��
v0
��ϵͳ��
2m1v0=m1v+m2vB
���
vB=
��vB=
�𣺣�1��A����2��4��2����3�����ɵ�һ�λָ���ԭ��ʱB���ٶ�Ϊ
��
��2������õ�������Ӻ���ԭ������ΪE=E1+��-
| 3 |
| 4 |
| E1 |
| 4 |
| E1 |
| 4 |
| 3 |
| 16 |
| E1 |
| 16 |
| E1 |
| n2 |
��3��A���鶯��Ϊ��̬��
| 1 |
| 4 |
��A������
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
��ã�v=��
| 1 |
| 2 |
��ϵͳ��
2m1v0=m1v+m2vB
���
vB=
| ||
| m2 |
| ||
| m2 |
�𣺣�1��A����2��4��2����3�����ɵ�һ�λָ���ԭ��ʱB���ٶ�Ϊ
| ||
| m2 |
| ||
| m2 |
��������1������ע�⡰����̫�������ǴӺ�ˮ����ȡԭ�ϣ���ˮ�����ͬλ��뮡�밺������㣻
��2�����⿼��Բ������۵������Ӧ���������Ѷ����У�
��3������ؼ����ݶ����غ㶨����ʽ������ʵ��������з�����
��2�����⿼��Բ������۵������Ӧ���������Ѷ����У�
��3������ؼ����ݶ����غ㶨����ʽ������ʵ��������з�����

��ϰ��ϵ�д�
�����Ŀ




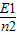 ��n=1��2��������E1��n=1ʱ�Ļ�̬��������һ��ԭ�ӷ�������Ϊ-
��n=1��2��������E1��n=1ʱ�Ļ�̬��������һ��ԭ�ӷ�������Ϊ-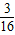 E1�Ĺ��Ӻ��ڱȻ�̬�����߳�-
E1�Ĺ��Ӻ��ڱȻ�̬�����߳�- E1�ļ���̬������ԭ�ӷ������ǰ���ڵ�______�ܼ���������Ӻ��ڵ�______�ܼ���
E1�ļ���̬������ԭ�ӷ������ǰ���ڵ�______�ܼ���������Ӻ��ڵ�______�ܼ��� ���ɵ�һ�λָ���ԭ��ʱB���ٶȣ�
���ɵ�һ�λָ���ԭ��ʱB���ٶȣ�