题目内容
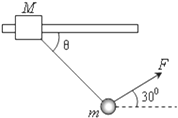
【题目】如图所示,质量![]() 的木块A套在水平杆上,并用轻绳将木块与质量
的木块A套在水平杆上,并用轻绳将木块与质量![]() 的小球B相连.今用跟水平方向成
的小球B相连.今用跟水平方向成![]() 角的力
角的力![]() ,拉着球带动木块一起向右匀速运动,运动中M、m相对位置保持不变,取
,拉着球带动木块一起向右匀速运动,运动中M、m相对位置保持不变,取![]() .求:
.求:
(1)运动过程中轻绳与水平方向夹角![]() ;
;
(2)木块与水平杆间的动摩擦因数为![]() .
.
(3)当![]() 为多大时,使球和木块一起向右匀速运动的拉力最小?
为多大时,使球和木块一起向右匀速运动的拉力最小?
【答案】(1)30°(2)μ=![]() (3)α=arctan
(3)α=arctan![]() .
.
【解析】
(1)对小球B进行受力分析,设细绳对N的拉力为T由平衡条件可得:
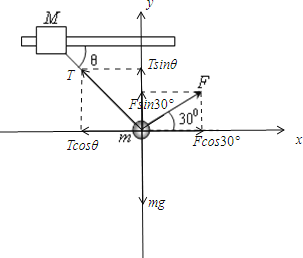
Fcos30°=Tcosθ
Fsin30°+Tsinθ=mg
代入数据解得:T=10![]() ,tanθ=
,tanθ=![]() ,即:θ=30°
,即:θ=30°
(2)对M进行受力分析,由平衡条件有
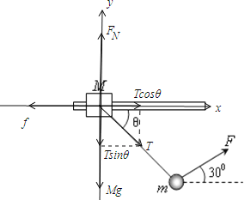
FN=Tsinθ+Mg
f=Tcosθ
f=μFN
解得:μ=![]()
(3)对M、N整体进行受力分析,由平衡条件有:
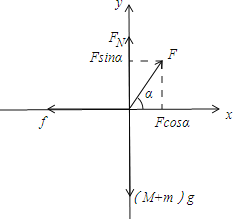
FN+Fsinα=(M+m)g
f=Fcosα=μFN
联立得:Fcosα=μ(M+m)g-μFsinα
解得:F=![]()
令:sinβ=![]() ,cosβ=
,cosβ=![]() ,即:tanβ=
,即:tanβ=![]()
则:![]()
所以:当α+β=90°时F有最小值.所以:tanα=μ=![]() 时F的值最小.即:α=arctan
时F的值最小.即:α=arctan![]()

练习册系列答案
 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目