Question

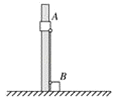
【题目】如图所示，A、B两滑块质量均为m，通过铰链用轻杆连接，让轻杆沿竖直方向，A套在固定的竖立直棒上、B放置在水平面上，A、B均静止。由于扰动，A开始向下运动，B沿水平面向右运动。滑块A、B可视为质点，重力加速度为g。在A向下运动的过程中，不计一切摩擦，可以证明：当轻杆转到与水平方向夹角θ满足sinθ=时，滑块A的机械能最小。试求：

(1)此时A的加速度大小；

(2)若杆的长度为L，从系统开始运动到A的机械能最小的过程中，杆对滑块B做的功。

Answer 1

【答案】(1)g (2)mgL

【解析】

根据能量关系分析加速度大小，然后由机械能守恒列出关系式根据题设临界情况解出所求结果

（1）滑块A从下滑到未着地前过程中，根据杆的弹力对AB做功情况可知A的机械能最小时杆的弹力为零，A在竖直方向仅受重力，故A此时的加速度aA＝g。

（2）设滑块A在下滑到杆与水平方向的夹角为θ时，二者速度大小分别为vA、vB，由系统机械能守恒得：

由于杆不可伸长和缩短，此时沿杆方向两滑块分速度相等，有：

vAsinθ＝vBcosθ

联立解得：

故sinθ＝时，有最大值．得：

对B分析，重力和水平面支持力不做功，根据动能定理得：杆的推力做功：