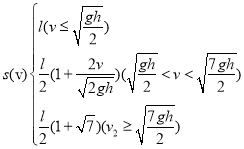题目内容
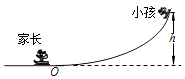
【题目】如图所示,AB是一段位于竖直平面内的光滑轨道,高度为h,末端B处的切线方向水平。一个质量为m的小物体P从轨道顶端A处由静止释放,滑到B端后飞出,落到地面上的C点,轨迹如图中虚线BC所示。已知它落地时相对于B点的水平位移OC=L。现在轨道下方紧贴B点安装一水平传送带,传送带的右端与B的距离为L/2。当传送带静止时,让P再次从A点由静止释放,它离开轨道并在传送带上滑行后从右端水平飞出,仍然落在地面的C点。当驱动轮转动从而带动传送带以速度v匀速向右运动时(其他条件不变),P的落地点为D。(不计空气阻力)
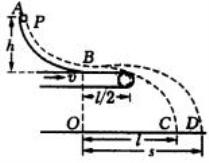
(1)求P滑至B点时的速度大小;
(2)求P与传送带之间的动摩擦因数 ;
(3)求出O、D间的距离s随速度v变化的函数关系式。
【答案】(1)![]() (2)
(2)![]()
(3)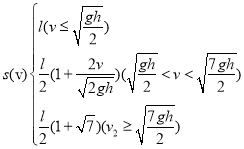
【解析】
试题分析:(1)物体P在AB轨道上滑动时,物体的机械能守恒,根据机械能守恒定律![]()
得物体P滑到B点的速度为:![]() 。
。
(2)当没有传送带时,物体离开B点后作平抛运动,运动时间为t,![]()
当B点下方的传送带静止时,物体从传送带右端水平抛出,落地的时间也为t,水平位移为![]() ,因此物体从传送带右端抛出的速度
,因此物体从传送带右端抛出的速度 ![]()
根据动能定理,物体在传送带上滑动时,有![]()
解出物体与传送带之间的动摩擦因数为 ![]()
(3)当传送带向右运动时,若传送带的速度v≤v 1 ,即![]() 时,物体在传送带上一直作匀减速运动,离开传送带的速度仍为v 1 ,落地的水平位移为
时,物体在传送带上一直作匀减速运动,离开传送带的速度仍为v 1 ,落地的水平位移为![]() ,即s=
,即s=![]() ;
;
当传送带的速度 ![]() 时,物体将会在传送带上做一段匀变速运动。如果尚未到达传送带右端,速度即与传送带速度相同,此后物体将做匀速运动,而后以速度v离开传送带。v的最大值v 2 为物体在传送带上一直加速而达到的速度,即
时,物体将会在传送带上做一段匀变速运动。如果尚未到达传送带右端,速度即与传送带速度相同,此后物体将做匀速运动,而后以速度v离开传送带。v的最大值v 2 为物体在传送带上一直加速而达到的速度,即![]()
由此解得: ![]() 。
。
当v≥v 2 ,物体将以速度![]() 离开传送带,因此得O、D之间的距离为
离开传送带,因此得O、D之间的距离为![]() 。
。
当v 1 < v < v 2 ,即![]() 时,物体从传送带右端飞出时的速度为v,O、D之间的距离为
时,物体从传送带右端飞出时的速度为v,O、D之间的距离为![]()
综合以上的结果,得出O、D间的距离s随速度v变化的函数关系式为